定義
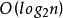 二項堆
二項堆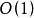 二項堆
二項堆二項堆是是二項樹的集合或是由一組二項樹組成。二項堆具有良好的性質。在 的時間內即可完成兩個二項堆合併操作,所以二項堆是可合併堆,而僅僅需要 的時間,二項堆即可完成插入操作。因此,基於二項堆實現的優先佇列和進程調度算法有著很好的時間性能。同時由於二項樹的結構特性和性質,二項樹在網路最佳化等諸多領域也套用廣泛 。
二項樹
二項樹是一種遞歸定義的有序樹,二項樹遞歸定義如下:
1、度數為0的二項樹只包含一個結點。
 二項堆
二項堆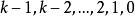 二項堆
二項堆2、度數為k的二項樹有一個根結點,根結點下有 個子女,每個子女分別是度數分別為 的二項樹的根。
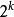 二項堆
二項堆 二項堆
二項堆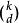 二項堆
二項堆度數為k的二項樹共有 個結點,高度為 。在深度d處有 (二項式係數)個結點。度數為k的二項樹可以很容易從兩顆度數為k-1的二項樹合併得到:把一顆度數為k-1的二項樹作為另一顆原度數為k-1的二項樹的最左子樹。這一性質是二項堆用於堆合併的基礎。
性質
二項堆是指滿足以下性質的二項樹的集合:
•每棵二項樹都滿足最小堆性質,即結點關鍵字大於等於其父結點的值
•不能有兩棵或以上的二項樹有相同度數(包括度數為0)。換句話說,具有度數k的二項樹有0個或1個。
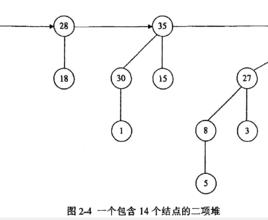
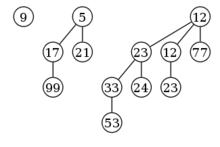 示例:一個含13個結點的二項堆
示例:一個含13個結點的二項堆 二項堆
二項堆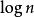 二項堆
二項堆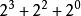 二項堆
二項堆以上第一個性質保證了二項樹的根結點包含了最小的關鍵字。第二個性質則說明結點數為 的二項堆最多只有 棵二項樹。實際上,包含n個節點的二項堆的構成情況,由n的二進制表示確定,其中每一位對應於一顆二項樹。例如,13的二進制表示為1101, , 因此具有13個節點的二項堆由度數為3, 2, 0的三棵二項樹組成,如圖。
操作
由於並不需要對二項樹的根結點進行隨機存取,因而這些結點可以存成鍊表結構。
合併
合併兩個二項堆示例,實際上把兩棵度數為1的二項樹合併為一棵度數為2的二項樹。
最基本的為二個度數相同的二項樹的合併。由於二項樹根結點包含最小的關鍵字,因此在二顆樹合併時,只需比較二個根結點關鍵字的大小,其中含小關鍵字的結點成為結果樹的根結點,另一棵樹則變成結果樹的子樹。
 二項堆
二項堆 二項堆
二項堆 二項堆
二項堆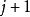 二項堆
二項堆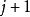 二項堆
二項堆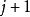 二項堆
二項堆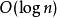 二項堆
二項堆兩個二項堆的合併則可按如下步驟進行:度數 從小取到大,在兩個二項堆中如果其中只有一棵樹的度數為 ,即將此樹移動到結果堆,而如果只兩棵樹的度數都為 ,則根據以上方法合併為一個度數為 的二項樹。此後這個度數為 的樹將可能會和其他度數為 的二項樹進行合併。因此,對於任何度數j,可能最多需要合併3棵二項樹。此操作的時間複雜度為 。
插入
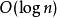 二項堆
二項堆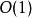 二項堆
二項堆創建一個只包含要插入元素的二項堆,再將此堆與原先的二項堆進行合併,即可得到插入後的堆。由於需要合併,插入操作需要 的時間。平攤分析的時間複雜度為 。
查找最小關鍵字所在結點
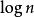 二項堆
二項堆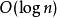 二項堆
二項堆由於滿足最小堆性質,只需查找二項樹的的根結點即可,因為一共有 棵子樹,所以用所時間為 。
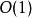 二項堆
二項堆可以保存一個指向最小元素的指針,使得查找最小關鍵字所在結點需要 的時間。在執行其他操作時,需要修改該指針。
刪除最小關鍵字所在結點
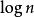 二項堆
二項堆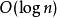 二項堆
二項堆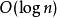 二項堆
二項堆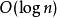 二項堆
二項堆先找到最小關鍵字所在結點,然後將它從其所在的二項樹中刪除,並獲得其子樹。將這些子樹看作(合併為)一個獨立的二項堆,再將此堆合併到原先的堆中即可。由於每棵樹最多有 棵子樹,創建新堆的時間為 。同時合併堆的時間也為 ,故整個操作所需時間為 。
減小特定結點(關鍵字)的值(Decreasing a key)
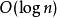 二項堆
二項堆在減小特定結點(關鍵字)的值後,可能會不滿足最小堆積性質。此時,將其所在結點與父結點交換,如還不滿足最小堆性質則再與祖父結點交換……直到最小堆性質得到滿足。操作所需時間為 。
刪除
將需要刪除的結點的關鍵字的值減小到負無窮大(比二項堆中的其他所有關鍵字的值都小即可),執行“減小關鍵字的值”算法,使其調整到當前二項樹的根節點位置,再刪除最小關鍵字的根結點即可。