定義
形式語言中一公式是可滿足的,若且唯若至少存在一個解釋,使該公式成為真命題。
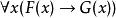 不可滿足性
不可滿足性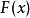 不可滿足性
不可滿足性 不可滿足性
不可滿足性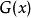 不可滿足性
不可滿足性 不可滿足性
不可滿足性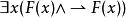 不可滿足性
不可滿足性例如:公式 是可滿足的,因為,如果令 表示“ 是人”, 表示“ 是要死的”,則在此解釋下,該公式即為命題“所有的人都是要死的”,這是個真命題。 而 是不可滿足的,因為不存在解釋使該公式成為真命題 。
相關分析
 不可滿足性
不可滿足性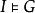 不可滿足性
不可滿足性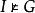 不可滿足性
不可滿足性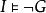 不可滿足性
不可滿足性對於一個變元自由的一階語言公式G,如果至少存在一個D論域上的一個解釋 ,在此解釋下G為真,則稱G是可滿足的,即 ;反之,如果對於任何解釋G均為假,則稱G是不可滿足的,即 或 。
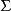 不可滿足性
不可滿足性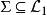 不可滿足性
不可滿足性 不可滿足性
不可滿足性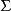 不可滿足性
不可滿足性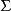 不可滿足性
不可滿足性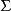 不可滿足性
不可滿足性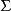 不可滿足性
不可滿足性對於一個變元自由的一階語言公式集 ,即 ,如果至少存在一個D的解釋,在此解釋下,的每個以D為論域的公式均為真,則稱為可滿足的;如果D的所有解釋都有假公式,則稱是不可滿足的。
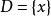 不可滿足性
不可滿足性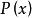 不可滿足性
不可滿足性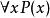 不可滿足性
不可滿足性 不可滿足性
不可滿足性 不可滿足性
不可滿足性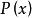 不可滿足性
不可滿足性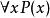 不可滿足性
不可滿足性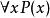 不可滿足性
不可滿足性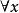 不可滿足性
不可滿足性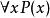 不可滿足性
不可滿足性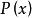 不可滿足性
不可滿足性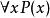 不可滿足性
不可滿足性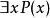 不可滿足性
不可滿足性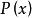 不可滿足性
不可滿足性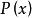 不可滿足性
不可滿足性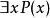 不可滿足性
不可滿足性需要注意,以上定義針對的是一個變元自由的公式。給定一個論域,可以定義的可滿足性和不可滿足性,而不能對定義它的可滿足性和不可滿足性。因為對命題的可滿足性可理解為從論域的最少量的變元樣本開始測試命題成立與否。用不滿D的全域的樣本(即〒)測試是可以的,但是不能測試,因為測試要用x的全部樣本,即。因此,必須是在給定論域D的全部樣本測試後才得到的,即的可滿足性是在之前做出的;而對於,可以認為是與有等同的可滿足性。因此可以說,在論域中是可滿足的,若且唯若是可滿足的。
歸結演繹方法
基本思路
歸結演繹方法是一種基於魯濱遜(Robinson)歸結原理的機器推理技術。魯濱遜歸結原理也稱作消解原理,是魯濱遜於1965年在海伯倫(Herbrand)理論的基礎上提出的一種基於邏輯的“反證法” 。
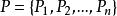 不可滿足性
不可滿足性 不可滿足性
不可滿足性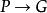 不可滿足性
不可滿足性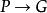 不可滿足性
不可滿足性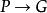 不可滿足性
不可滿足性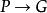 不可滿足性
不可滿足性在人工智慧中幾乎所有的問題都可以轉化為一個定理證明問題。而定理證明的實質就是要從公式集出發推出結論G,即需要證明永真。要證明永真,若按定義來,需要證明在任何一個非空的個體域上都是永真的。這將是非常困難的,甚至是不可實現的。為此人們進行了大量的探索,後來發現可以採用反證法的思想,把關於永真性的證明轉化為關於不可滿足性的證明。即要證明永真,只要能夠證明是不可滿足的就可以了。在這一方面最有成效的工作就是海伯倫理論和魯濱遜歸結原理。魯濱遜歸結原理使定理證明的機械化成為了現實。他們這些研究成果,在人工智慧的發展史上都占有很重要的歷史地位。
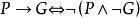 不可滿足性
不可滿足性(1)我們首先需證明式成立,永真性的證明可以化為不可滿足性的證明。
由命題邏輯的基本知識可得表1。
| P | G | 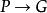 不可滿足性 不可滿足性 | 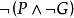 不可滿足性 不可滿足性 |
| F | F | T | T |
| F | T | T | T |
| T | F | F | F |
| T | T | T | T |
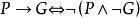 不可滿足性
不可滿足性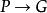 不可滿足性
不可滿足性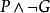 不可滿足性
不可滿足性從表1可知:,從而永真性的證明可以化為的不可滿足性的證明。
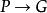 不可滿足性
不可滿足性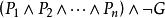 不可滿足性
不可滿足性(2)要驗證即不可滿足,只需要驗證以上公式中的任意一個子式不可滿足即可。
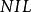 不可滿足性
不可滿足性 不可滿足性
不可滿足性我們定義不包含任意文字的子句為空子句,空子句是永假的,不可滿足的,一般記為或。由子句和空子句組成的集合稱為子句集。
在謂詞邏輯中,任何一個謂詞公式都可以通過套用等價關係及推理規則化成相應的子句集,且子句集無量詞約束、元素只是文字的析取、否定符只作用於單個文字,元素間默認為合取。
(3)歸結:我們定義命題P為文字,¬P和P為互補文字。設C和C是子句集S中的任意兩個子句,如果子句C中的文字L與C中的文字L互補,則可從C和C中分別消去L和L,並將兩個子句餘下的部分析取構成一個新子句C。我們稱這一過程為歸結,C為C和C的歸結式,C和C為C的親本子句。
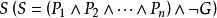 不可滿足性
不可滿足性即魯濱遜歸結原理的基本思路是:已知P,證明G,首先把欲證明的結論否定(¬G),並加入前件知識構成子句集S(S=),化子句集S;設法檢驗子句集S中是否有空子句,若含有空子句,則S是不可滿足的;若不含有空子句,則繼續使用歸結運算,對S中的子句進行歸結至導出空子句或不能繼續歸結為止。
使用步驟
運用歸結原理證明定理的過程稱為歸結反演。已知F,證明G的歸結反演過程及步驟如下:
(1)首先把欲證明的結論(目標公式)G否定得到¬G;
(2)並把¬G加入公式集F中,得{F,¬G};
(3)把{F,¬G}化成子句集S;
(4)運用歸結原理對S中的子句進行歸結,並將歸結式加入S,反覆進行,直到歸結至導出空子句為止。
完備性
歸結原理的歸結過程是完備的:因為子句集S是不可滿足的,充要條件是存在一個從S到空子句的歸結過程。
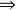 不可滿足性
不可滿足性我們知道:設C和C是子句集S中的任意兩個子句,C是C和C的歸結式,若用C代替C和C後,構成新的子句集S,則由S的不可滿足性可以推出S的不可滿足性,即S不可滿足S不可滿足。
 不可滿足性
不可滿足性設C和C是子句集S中的任意兩個子句,C是C和C的歸結式,若將C添加到S中構成新的子句集S,則由S的不可滿足性與S的不可滿足性等價,即S不可滿足S不可滿足。
進而我們可以利用新子句集S和S不可滿足推出S不可滿足。從而只要能從S歸結出空子句,子句集S就是不可滿足的;子句集S是不可滿足的,就一定存在一個從S到空子句的歸結過程。此歸結具有完備性。
歸結過程
在謂詞邏輯下求兩個子句的歸結式,和命題邏輯一樣是消互補對,但需考慮變數的合一與置換。簡單討論一階謂詞邏輯描述下的歸結推理方法,謂詞邏輯的歸結過程與命題邏輯的歸結過程相比,其基本步驟相同,但每步的處理對象不同。謂詞邏輯需要把由謂詞構成的公式集化為子句集,必要時在得到歸結式前要進行置換和合一。
具體的謂詞邏輯歸結過程如下:
(1)寫出謂詞關係公式;
(2)用反演法寫出謂詞表達式;
(3)化為Skolem標準形;
(4)求取子句集S;
(5)對S中可歸結的子句做歸結;
(6)歸結式仍放入S中,反覆歸結過程;
(7)得到空子句;
(8)命題得證 。

