三角形界心

三角形界心 如果三角形一邊上的一點和這邊所對的頂點把三角形的周界分割為兩條等長的折線，那么就稱這一點為三角形的周界中點。

定義1

如果三角形一邊上的一點和這邊所對的頂點把三角形的 周界分割為兩條等長的折線，那么就稱這一點為 三角形的周界中點。其中 三角形的周界是指有三角形的三邊所組成的圍線。

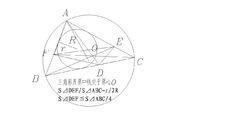三角形界心

周界中點性質：三角形任意一邊上的周界中點必介於這邊兩端點之間。（此由“三角形的任意兩邊之和大於第三邊”可知）

定義2

三角形的頂點與其對邊的 周界中點的連線叫做 三角形的周界中線。

有時亦稱周界中線所在直線為三角形的周界中線。

周界中線性質：三角形三條周界中線交於一點。

定義3

三角形三條周界中線的交點叫做 三角形的界心。

三角形界心性質：設點D、E、F分別為⊿ABC的BC、CA、AB邊上的周界中點，R、r分別為⊿ABC的外接圓和內切圓的半徑，則

（1）S⊿DEF/S⊿ABC=r/2R；

（2）S⊿DEF≦S⊿ABC/4。