銀行間市場七天回購移動平均利率(即原來的“基準利率參考指標”,下簡稱移動平均利率)的數據基礎是銀行間市場7天回購利率(R007),R007是統計意義上的綜合品種,實際涵蓋了回購期限為2、3、4、5、6、7天的質押式回購交易,這是一種約定俗成的定義,符合市場慣例。計算過程包括異常數據處理、日加權數據生成和計算移動平均利率三個階段。
一、異常數據的處理
在回購市場上異常交易是難免的,事實證明也的確如此。異常交易的存在會導致價格扭曲,擾亂正常的市場秩序,因此為了能夠展現真實的市場行情對異常交易進行處理是極其必要的。處理異常交易的手段往往與交易數據本身的特點聯繫在一起的,因此手段往往也是多種多樣。
針對銀行間7天回購交易的實際情況,我們採用了“削頭去尾”的處理方法,即在參與當天計算的全部交易當中,去掉一個最高價和一個最低價;碰到不止一個最高價和不止一個最低價的情況,則去掉成交量最小的那一個;如果僅有兩筆交易參與計算,則不做任何處理。因此,如果某一交易日 ,在計算時候共有 筆交易發生,在去掉一個最高價和最低價以後,剩下的 筆交易就是生成日加權回購利率的數據基礎了,為了敘述方便,不妨假設這 筆交易的價格(回購利率)和成交量(回購量)分別為 和 ,下標 代表某一個確定的交易日,下標 代表該交易日該時刻的第 筆交易,顯然 。
下表直觀地給出了異常數據處理的一般準則,處理以後的交易筆數。同時,從表中可以看出,對應最高價0.02115的交易共有兩筆,剔除的正是交易量最小的那一筆。
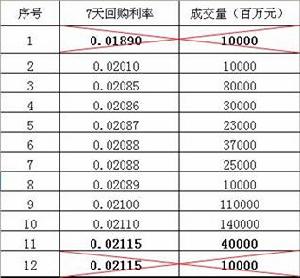
在剔除異常交易數據以後,我們得到了兩個時間序列,一個是價格序列 ,一個是交易量序列 ,這兩個序列的元素個數均為 個,也就是 筆交易。為了得到 日該計算時刻對應的代表性利率指標 ,我們採用成交量加權的做法,
每一個價格前面的權重為 。
如此以來,對於每一個交易日的每次計算,我們都會得到一個回購利率的日加權 ,隨著交易的繼續和每隔5分鐘一次的計算此日的加權 不斷更新,形成一個序列 ,這就是我們非常熟悉的7天回購日加權利率。每天閉市後,隨著交易的中斷,計算終止,產生的 為當天的最終日加權 ,保存後不在更新。
仍然以上面的表格為例,在去掉一個最高、最低價之後,有效交易筆數為 ,按照成交量加權算法即得
0.020967即為當日當時的日加權回購利率。
三、以移動平均算法來生成基準利率
從原理上講,每天每刻的日加權利率都揭示了當日當時的利率行情,因此也就具備了充當市場基準利率(Benchmark)的可能性,然而作為一個基準利率,穩定性也是不可或缺的。事實上,從7天回購利率的歷史統計來看,歷史的日均加權利率的波動性還是比較大的,為了追求基準利率的平穩性,必須要綜合最近一段時間的日加權利率來進行適度的光滑,常見的光滑算法有簡單算術平均和指數加權平均兩種。
因為每一個交易日都對應一個7天回購的日加權利率,為了得到一個穩定的基準利率,只能藉助過去的7天回購日加權利率,譬如,為了得到 日的移動平均利率,我們必須要利用前一天( )、前二天( )…的日加權利率,不妨假設共有 個,即 ,如L=10代表的是 日前(不包括 日)的10個交易日。這裡歷史區間跨度 的大小與我們的目標有關, 越大光滑性越好; 越小波動性越強,但往往更貼近當前的利率行情。為了敘述方便,我們以 來表示與 有關的第 天的移動平均利率。
(一)算術加權平均
算術加權平均的思路是每一個價格前面的權重是相同的,對每一個價格都“一視同仁”,每個價格蘊涵的信息量完全一樣。算術加權平均具有簡單直觀、計算方便的優點。計算公式如下:
(二)指數加權平均(EWMA)
指數加權平均的基本思想是價格序列採用指數加權的形式,每個價格前的權重是不同的,離現在越近的利率其權重越大,表示對其越重視,離現在越遠的利率其權重越小,表示對其越不重視。指數加權平均暗含的假設是當前價格與不同的歷史數據依賴程度是不一樣的,應該“區別對待”。指數加權平均強調了信息的不對稱性,從預測意義上來說,指數加權平均更符合金融時間序列的有關理論。
衰減因子是指數加權平均的一個十分關鍵的要素,衰減因子通常用 表示,它通常是一個大於0小於1的一個數,即 ,每個價格前面的權重是 的冪次,離現在越近的冪次越小,離現在越遠的冪次越大,由於 是一個大於0小於1的一個數,其冪次越高值就越小,也就是說離現在越近的權重越大,離現在越遠的權重越小,由此就達到了指數加權平均“區別對待”的效果。指數加權平均的計算公式如下:
衰減因子 的選取不單單是一個技術問題,還必須兼顧到業務的背景。在根據歷史數據跨度 來確定衰減因子時,我們遵循了下面的公式:
譬如,當 時, ;當 時, ,於是,不同的 的對應了不同的移動平均利率。
舉例來說明,假設 天的7天回購日,它前面10天的加權利率數據已經在下表中列出。現在要用指數加權平均算法來計算 天對應的移動平均利率,首先要確定10對應的衰減因子,通過上面衰減因子的估算公式很容易得到衰減因子為0.905,然後以它的冪次為權重來對歷史數據加權即得到表的最後一行,最後除以各冪次的和,就可計算出 天對應的移動平均利率0.020936。
| 日期 | |||
| t-10 | 0.0219 | 0.3685 | 0.0081 |
| t-9 | 0.0204 | 0.4072 | 0.0083 |
| t-8 | 0.0212 | 0.4500 | 0.0095 |
| t-7 | 0.0212 | 0.4972 | 0.0105 |
| t-6 | 0.0209 | 0.5494 | 0.0115 |
| t-5 | 0.0209 | 0.6071 | 0.0127 |
| t-4 | 0.0209 | 0.6708 | 0.0140 |
| t-3 | 0.0207 | 0.7412 | 0.0154 |
| t-2 | 0.0209 | 0.8190 | 0.0171 |
| t-1 | 0.0209 | 0.9050 | 0.0189 |
注意:計算某天的移動平均利率所採用的數據為該天前的一段時間內的加權,不包括該天!
在每天交易結束、收盤之後,便可以計算下一個交易日的移動平均利率,這樣就能保證在每個交易日開盤之前當日的移動平均利率已經存在,為基準調整日的應計利息的計算帶來方便。
四、移動平均利率品種含義
通過中國貨幣網等平台發布的移動平均利率目前共有6種,它們的含義如下
| 七天回購移動平均利率 | 算術加權 | 指數加權 |
| 日加權 | B0 | B0 |
| 最近2周的加權 | B_2W | B2W |
| 最近1月的加權 | B_1M | B1M |
| 最近2月的加權 | B_2M | B2M |
| 最近3月的加權 | B_3M | B3M |
| 最近6月的加權 | B_6M | B6M |
這裡的日加權BO展現的是當天當時的加權利率,隨著時間的推移,B0的值在變化,一直到每天的閉市。這裡的1個禮拜(1W)等於5個交易日,2個禮拜(2W)等於10個交易日;1個月(1M)等於20個交易日,2個月(2M)等於40個交易日(注意這X交易日即當日的前X天,不包括當天),其它依次類推。
可通過歷史數據欄目獲得各移動平均利率品種數據。
B_iM(W)表示最近i個月(周)的簡單算術平均;BiM(W)表示最近i個月(周)的指數加權平均
