局部線性嵌入算法(locallylinearembedding,LLE)
局部線性嵌入算法(locallylinearembedding,LLE)是解決降維的方法,針對LLE計算速度和近鄰點個數K的選取,研究了該方法的擴展,提出了基於聚類和改進距離的LLE方法.基於聚類LLE方法大大縮減了計算LLE方法的時間;改進距離的LLE方法在近鄰點個數取值比較小時的情況下,可得到良好的效果,而原始的LLE方法要達到相同的效果,近鄰點個數K的取值通常要大很多.同時,改進距離的LLE方法可以模糊近鄰點個數選取.實驗結果表明,基於聚類和改進距離相結合的LLE方法相比原來的LLE方法大大提高了降維速度和擴大了參數K的選取.
LLE及其改進算法介紹
Locallylinearembedding(LLE)(SamT.RoweisandLawrenceK.Saul,2000)以及Supervisedlocallylinearembedding(SLLE)(DickandRobert,2002)是最近提出的非線性降維方法,它能夠使降維後的數據保持原有拓撲結構。
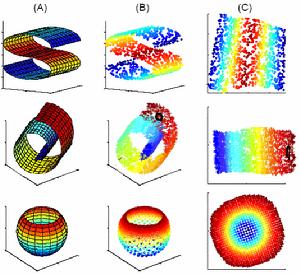
LLE算法可以有圖1所示的一個例子來描述。在圖1所示中,LLE能成功地將三維非線性數據映射到二維空間中。如果把圖1(B)中紅顏色和藍顏色的數據分別看成是分布在三維空間中的兩類數據,通過LLE算法降維後,則數據在二維空間中仍能保持相對獨立的兩類。在圖1(B)中的黑色小圈中可以看出,如果將黑色小圈中的數據映射到二維空間中,如圖1(C)中的黑色小圈所示,映射後的數據任能保持原有的數據流形,這說明LLE算法確實能保持流形的領域不變性。由此LLE算法可以套用於樣本的聚類。而線性方法,如PCA和MDS,都不能與它比擬的。LLE算法操作簡單,且算法中的最佳化不涉及到局部最小化。該算法能解決非線性映射,但是,當處理數據的維數過大,數量過多,涉及到的稀疏矩陣過大,不易於處理。在圖1中的球形面中,當缺少北極面時,套用LLE算法則能很好的將其映射到二維空間中,如圖1中的C所示。如果數據分布在整個封閉的球面上,LLE則不能將它映射到二維空間,且不能保持原有的數據流形。那么我們在處理數據中,首先假設數據不是分布在閉合的球面或者橢球面上。
 LLE
LLE圖1非線性降維實例:B是從A中提取的樣本點(三維),通過非線性降維
算法(LLE),將數據映射到二維空間中(C)。從C圖中的顏色可以看出
通過LLE算法處理後的數據,能很好的保持原有數據的鄰域特性
LLE算法是最近提出的針對非線性數據的一種新的降維方法,處理後的低維數據均能夠保持原有的拓撲關係。它已經廣泛套用於圖像數據的分類與聚類、文字識別、多維數據的可視化、以及生物信息學等領域中。
1LLE算法
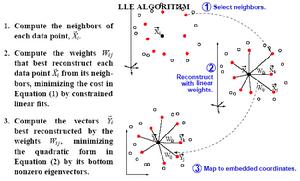
LLE算法可以歸結為三步:(1)尋找每個樣本點的k個近鄰點;(2)由每個樣本點的近鄰點計算出該樣本點的局部重建權值矩陣;(3)由該樣本點的局部重建權值矩陣和其近鄰點計算出該樣本點的輸出值。具體的算法流程如圖2所示。
 LLE
LLE