概述
2-3樹是最簡單的B-樹(或-樹)結構,其每個非葉節點都有兩個或三個子女,而且所有葉都在統一層上。2-3樹不是二叉樹,其節點可擁有3個孩子。不過,2-3樹與滿二叉樹相似。若某棵2-3樹不包含3-節點,則看上去像滿二叉樹,其所有內部節點都可有兩個孩子,所有的葉子都在同一級別。另一方面,2-3樹的一個內部節點確實有3個孩子,故比相同高度的滿二叉樹的節點更多。高為h的2-3樹包含的節點數大於等於高度為h的滿二叉樹的節點數,即至少有2^h-1個節點。換一個角度分析,包含n的節點的2-3樹的高度不大於[log2(n+1)](即包含n個節點的二叉樹的最小高度)。
例如,下圖顯示高度為3的2-3樹。包含兩個孩子的節點稱為2-節點,二叉樹中的節點都是2-節點;包含三個孩子的節點稱為3-節點。
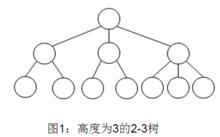 2-3樹
2-3樹將數據項放入2-3樹節點中的規則是:
(1)2-節點有兩個孩子,必含一個數據項,其查找關鍵字大於左孩子的查找關鍵字,而小於右孩子的查找關鍵字。
(2)3-節點有三個孩子 ,必含兩個數據項,其查找關鍵字S和L滿足下列關係:S大於左孩子的查找關鍵字,而小於中孩子的查找關鍵字;L大於中孩子的查找關鍵字,而小於右孩子的查找關鍵字。
(3)葉子可以包含一個或兩個數據項。
2-3樹的基本運算
遍歷2-3樹
可通過類似於中序遍歷的方式。按有序的查找關鍵字順序遍歷2-3樹 ,代碼如下:
inorder(in ttTree:TwoThreeTree)
//Traverse the noneempty 2-3 tree ,ttTree in sorted
//search-key order
{
if(ttTree's root node r is a leaf)
visit the data items
else if(r has two data items)
{
inorder(left subtree of ttTree's root);
visit the first data item
inorder(middle subtree of ttTree's root);
visit the last data item
inorder(right subtree of ttTree's root);
}
else
{
inorder(left subtree of ttTree's root)
visit the first data item
inorder(middle subtree of tttree's root);
}
}
查找2-3樹
2-3樹中的節點排序與二叉樹中的排序相似,允許在2-3樹中有效地查找某一項。實際上,有下面的偽碼可以看到,2-3樹的檢索操作非常類似與二叉樹的檢索操作。
代碼如下:
retrieveItem(in ttTree: TwoThreeTree,in searchKey :keyType,
out treeItem:TTreeItemType):boollean
//retrieve into treeItem from a noneempty 2-3 tree ttTree
//the item whose search key equals searchkey,the operation fails if no
//such item exists ,the function returns true if the item is found ,
//false otherwise
{
if(searchKey is in ttTree's root node r)
{
treeItem =the data portion of r
return true;
}
else if(r is a leaf)
{
return false;
}
else if(r has two data items)
{
if(searchKey<smaller search key of r)
return retrieve(r's left subtree,searchkey,treeitem)
else if(searchKey<larger search key of r)
return retrieve(r's middle subtree ,searchKey,
treeItem);
else
return retrieve(r's right subtree,searchKey,
treeItem)
}
else
{
if(searchKey<r's search key)
return retrieve(r's left subtree,searchKey,treeItem);
else
return retrieve(r's middle subtree,searchKey,treeItem);
}
}
插入算法
要將項I插入2-3樹,首先定位查找I的操作將終止的葉子。將新項I插入葉子,若當前葉子包含兩個項目,則任務完成。但若葉子包含三個項,則必須將其分為兩個節點n1和n2。將最小項S放在n1,將最大項放在n2,將中間項M上移到葉子的雙親。結果,節點n1和n2成為雙親的孩子。若雙親只有三個孩子,並包含兩個項目,則任務完成。但是,若雙親當前有四個孩子,並包含有三項,則需要拆分。
上述葉子操作的過程,拆分包含三個項的內部節點n,但必須考慮n的四個孩子。如圖5所示,將n拆分為n1和n2,將n的最小項S放到n1,將n左面的兩個孩子關聯到n1。將n的最大項L放入n2,將n右邊的兩個孩子關聯到n2,將n的中間項M上移到n的雙親。
此後,拆分節點和將項上移到雙親的過程遞歸地進行,知道遇到這樣一個節點:再插入前,它只有一個項,而在接納新項後,只有兩個項。注意,在前面的插入序列中,樹的高度保持不變,一直是原始3 。一般情況下,只要在從根到插入新項的葉子的路徑上,至少有一個節點只包含一個項,則插入將不會增加樹的高度。因此,與基本二叉查找樹的策略相比,2-3樹的插入策略推遲了樹的高度的增長。
當2-3樹的高度增長時,則從項的頂部向下完成。如果從根到插入新項的葉子的路徑上,每個節點包含兩個項,則2-3樹的高度將增長。在這種情況下,拆分節點以及將項上移到節點雙親的遞歸過程最終到達根r。此時,向其他任何內部節點一樣,必須為r拆分為r1和r2。不過,必須新建一個包含r的中間項的節點,是這個節點成為n1和n2的雙親的節點。於是,新節點成為樹的新項。
代碼如下:
retrieveItem(in ttTree: TwoThreeTree,in searchKey :keyType,
out treeItem:TTreeItemType):boollean
//retrieve into treeItem from a noneempty 2-3 tree ttTree
//the item whose search key equals searchkey,the operation fails if no
//such item exists ,the function returns true if the item is found ,
//false otherwise
{
if(searchKey is in ttTree's root node r)
{
treeItem =the data portion of r
return true;
}
else if(r is a leaf)
{
return false;
}
else if(r has two data items)
{
if(searchKey<smaller search key of r)
return retrieve(r's left subtree,searchkey,treeitem)
else if(searchKey<larger search key of r)
return retrieve(r's middle subtree ,searchKey,
treeItem);
else
return retrieve(r's right subtree,searchKey,
treeItem)
}
else
{
if(searchKey<r's search key)
return retrieve(r's left subtree,searchKey,treeItem);
else
return retrieve(r's middle subtree,searchKey,treeItem);
}
}
