歐拉的質數多項式
歐拉的質數多項式如下：
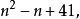黑格納數在n=1,...,40時會產生不同的40個質數，這相關於黑格納數163=4·41−1.
黑格納數歐拉公式， 取值為1,... 40和以下的多項式
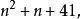黑格納數 黑格納數讓 取值0,... 39時等效，而Rabinowitz證明了
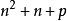黑格納數
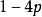黑格納數
黑格納數在 時，多項式為質數的充份必要條件為其判別式 等於負的黑格納數。
黑格納數
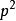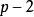黑格納數
黑格納數（若代入 會得到 一定不是質數，因此最大值只能取到 ）
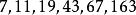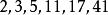黑格納數
黑格納數1, 2和3不符合要求，因此符合條件的黑格納數為 ，也就表示可以讓歐拉公式產生質數的p為 ，這些數字被弗朗索瓦·勒·利奧奈稱為歐拉的幸運數。
拉馬努金常數
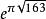黑格納數拉馬努金常數是 的值，是超越數，但非常接近整數：
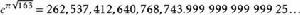黑格納數這個數字是在1859年由數學家夏爾·埃爾米特發現，在1975年愚人節的《科學美國人》，《數學遊戲》的專欄作家馬丁·加德納故意聲稱這個數字其實是整數，而印度數學天才斯里尼瓦瑟·拉馬努金也預測了這個數很接近整數，因此以他的名字來命名。
這個巧合可以用j-invariant的複數乘法及q展開來表示。
註解
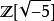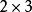黑格納數
黑格納數
黑格納數Q(√−d)的整數環為唯一分解整環，也就表示Q(√−d)的數字都只有一種因數分解方式，例如Q(√−5)的整數環不是唯一分解整環，因為6可以以兩種方式在 中表成整數乘積： 和 。
