基本介紹
 頻率直方圖
頻率直方圖 頻率直方圖
頻率直方圖 頻率直方圖
頻率直方圖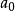 頻率直方圖
頻率直方圖 頻率直方圖
頻率直方圖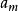 頻率直方圖
頻率直方圖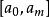 頻率直方圖
頻率直方圖設 是總體的樣本,其最小值記為 ,最大值記為b,又設 是小於 的最大整數, 是大於b的最小整數,將區間 等分成m個小區間
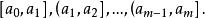 頻率直方圖
頻率直方圖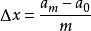 頻率直方圖
頻率直方圖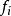 頻率直方圖
頻率直方圖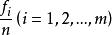 頻率直方圖
頻率直方圖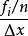 頻率直方圖
頻率直方圖 頻率直方圖
頻率直方圖 頻率直方圖
頻率直方圖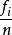 頻率直方圖
頻率直方圖 頻率直方圖
頻率直方圖 頻率直方圖
頻率直方圖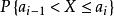 頻率直方圖
頻率直方圖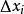 頻率直方圖
頻率直方圖 頻率直方圖
頻率直方圖顯然,各小區間的長度均為 ,然後統計出樣本觀測值落入各小區間的頻數 ,並計算頻率 。以每個小區間為底,以 為高在平面直角坐標系內作小矩形,這些小矩形組成的圖形稱為 頻率直方圖。顯然第 個小矩形的面積恰好是樣本觀測值落人第 個小區間內的頻率 。若總體X的機率密度為 ,則X的觀測值落入第 個小區間內的機率為 ,其幾何意義是以 為底,機率密度曲線 為頂的曲邊梯形的面積,於是有
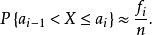 頻率直方圖
頻率直方圖因此,當樣本容量n無限增大時,頻率直方圖的階梯形折線將逼近於機率密度曲線。也就是說,當n充分大時,頻率直方圖近似地反映了機率密度曲線的大致形狀,在統計推斷中常常由此提出對總體分布形式的假設 。
例題解析
【例1】某地區連續50年中四月份平均氣溫資料如下(單位:℃):
6.9 4.1 6.6 5.2 6.4 7.9 8.6 3.0 4.4 6.7
7.1 4.7 9.1 6.8 8.6 5.2 5.8 7.9 5.6 8.8
8.1 5.7 8.4 4.1 6.4 6.2 5.2 6.8 5.6 5.6
6.8 8.2 6.4 4.8 6.9 7.1 9.7 6.4 7.3 6.8
7.1 4.8 5.8 6.5 5.9 7.3 5.5 7.4 6.2 7.7
以上述資料為依據,推斷該地區四月份平均氣溫的分布類型。
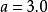 頻率直方圖
頻率直方圖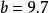 頻率直方圖
頻率直方圖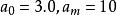 頻率直方圖
頻率直方圖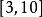 頻率直方圖
頻率直方圖解: 樣本觀測值中最小值 ,最大值 ,取 。將區間 等分為7個小區間,區間長度為1,計算樣本觀測值落人各小區間的頻數與頻率,見表1。
| 區間 | 頻數 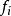 頻率直方圖 頻率直方圖 | 頻率 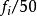 頻率直方圖 頻率直方圖 |
| [3,4] | 1 | 1/50 |
| (4,5] | 6 | 6/50 |
| (5,6] | 11 | 11/50 |
| (6,7] | 15 | 15/50 |
| (7,8] | 9 | 9/50 |
| (8,9] | 6 | 6/50 |
| (9,10] | 2 | 2/50 |
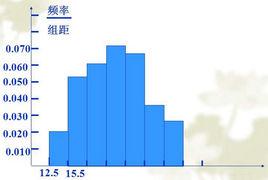
根據表1作出頻率直方圖,見圖1,由直方圖可見,該地區四月份平均氣溫近似服從常態分配。
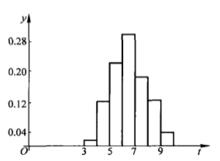 圖1
圖1這個結論僅僅是對樣本數據的統計分析,對總體分布形式提出了一個假設,它是否符合實際,還要進行檢驗 。
解題注意:可以根據縱軸標示區分是頻數直方圖還是頻率直方圖。
難點:從頻率直方圖得到數字特徵(均值、中位數、眾數等)。
【例2】將容量為n的樣本中的數據分成6組,繪製頻率分布直方圖,若第一組至第六組數據的頻率之比為2:3:4:6:4:1,且前三組數據的頻數之和等於27,則n等於( )。
(A)80 (B)75 (C)70 (D)65 (E)60
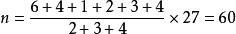 頻率直方圖
頻率直方圖解: 頻率=頻數/總數,所以頻率之比=頻數之比,所以容量,選(E) 。
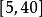 頻率直方圖
頻率直方圖【例3】某棉紡廠為了了解一批棉花的質量,從中隨機抽取了100根棉花纖維的長度(棉花纖維的長度是棉花質量的重要指標),所得數據都在區間中,其頻率分布直方圖如圖2所示,則其抽樣的100根中,棉花纖維的長度小於20mm的約有( )根。
(A)18 (B)20 (C)22 (D)25 (E)30
解:小於20 mm的頻率之和為(0.01+0.01+0.04)×5=0.3,所以100根中有30根,選E 。