簡介
類似靜電場，對電流場也可以通過引入“電流線” 來進行形象描述。電流線即電流所在空間的一組曲線， 其上任一點的切線方向和該點的電流密度方向一致。一束這樣的電流線圍成的管狀區域稱為電流管。
電流強度和電流密度
中學裡接觸到直流電路的時候，曾引入電流強度：
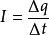電流管電流強度的單位為庫侖/秒，稱為安[培]，符號為A。
用電流強度描述導體中電荷的巨觀流動性質似乎太“粗糙”。
（1）不能描述電流沿截面的分布情況；
（2）不能描述電流的方向，即正電荷移動的方向。
為了描述導體中各點電流的大小和方向，人們引入一個更“精細”的物理量——電流密度。
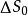電流管
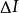電流管電流密度的定義：考慮導體中某一給定點P，在該點沿電流方向作一單位矢量n，並取一面元與n垂直，如圖所示。設通過 的電流強度為 ，則定義P點處電流密度的大小為：
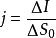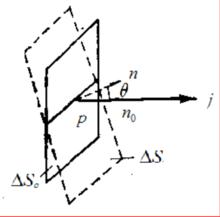電流管
電流管單位為安培/米 （A·m ）。
為了使電流密度能同時表示出P點處電流的方向，可將電流密度定義為一個矢量，其方向與n同向，表示正電荷移動的方向，即：
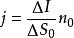電流管電流密度是矢量, 它在導體中任意一點的方向與正載流子在該點的流動方向相同，它的大小等於通過該點並垂直於電流的單位截面的電流強度。
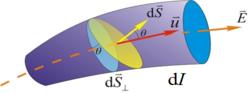電流管電流場
由上述定義可見，電流密度是一個矢量，它的方向表示導體中某點電流的方向，數值等於通過垂直於該點電流方向的單位面積的電流強度。這樣定義的電流密度是空間位置的矢量函式j(r)，它細緻地描述了導體中的電流分布，也稱為電流場。
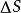電流管
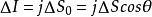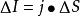電流管
電流管已知導體中某點P的電流密度，可以求得通過該點任一面元 的電流強度 。（見上頁圖）又可寫成 。
通過 S 面的電流強度I ：
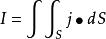電流管電流線
為形象描述電流場中電流的分布，實際為電流密度矢量線。
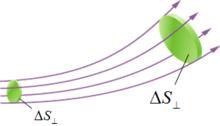電流管穩恆條件
從電流連續方程出發，立刻可導出穩恆電流應滿足的條件。對穩恆電流來說，導體內各點電流密度應與時間無關，要求dq/dt與時間無關，如果不為零，則造成電荷不斷積累，電場隨時間變化，將破壞電流的穩定，所以
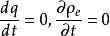電流管於是，
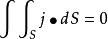電流管或，
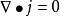電流管稱做穩恆條件的積分形式和微分形式。穩恆條件表明，電荷分布將不會因穩恆電流的存在而隨時間變化，所以由它產生的電場必然是靜電場。
藉助於電流線和電流管的概念，可以對穩恆條件作如下形象解釋：
（1）電流線不可能有起點和終點，即穩恆電流的電流線或電流管一定是閉合的；
（2）沿任一電流管各截面的電流強度都相等。
通常的直流電路由導線連線而成，電流線沿著導線分布，從而導線本身就是一個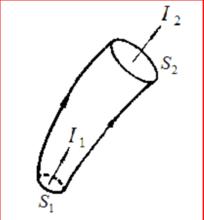電流管。
電流管由上述結論可知，直流電路（或者說穩恆電路）應當是閉合的；且沿一段沒有分支的電路，各處的電流強度必定相等。
