定義
定義1
流體運動中慣性力對黏滯力比值的無量綱數Re=UL/ν 。其中U為速度特徵尺度，L為長度特徵尺度，ν為運動學黏性係數。
所屬學科：大氣科學（一級學科）；動力氣象學（二級學科）
定義2
表征流體運動中黏性作用和慣性作用相對大小的無因次數。
所屬學科：電力（一級學科）；通論（二級學科）
定義3
衡量作用於流體上的慣性力與黏性力相對大小的一個無量綱相似參數，用Re表示，即Re=ρvl/η，式中ρ——流體密度；v——流場中的特徵速度；l——特徵長度；η——流體的黏性係數。
所屬學科：航空科技（一級學科）；飛行原理（二級學科）
定義4
表征流體運動中黏性作用和慣性作用相對大小的無因次數。
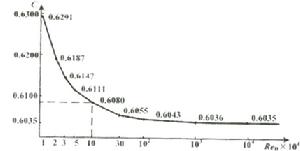
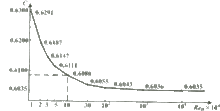孔板流出係數隨雷諾數變化所屬學科：水利科技（一級學科）；水力學、河流動力學、海岸動力學（二級學科）；水力學（水利）（三級學科）
相同注釋
含義
雷諾數就是表征流體流動特性的一個重要參數。
表達式
測量管內流體流量時往往必須了解其流動狀態、流速分布等。流體流動時的慣性力Fg和粘性力(內摩擦力)Fm之比稱為雷諾數。用符號Re表示。Re是一個無因次量。
式中的動力粘度η用運動粘度υ來代替，因η=ρυ，則
式中：
l υ——流體的平均速度；
l l——流束的定型尺寸；
l ρ、η一一在工作狀態；流體的運動粘度和動力粘度
l ρ——被測流體密度；
由上式可知，雷諾數Re的大小取決於三個參數，即流體的速度、流束的定型尺寸以及工作狀態下的粘度。
用圓管傳輸流體，計算雷諾數時，定型尺寸一般取管道直徑(D)，則用方形管傳輸流體，管道定型尺寸取當量直徑(Dd)。當量直徑等於水力半徑的四倍。對於任意截面形狀的管道，其水力半徑等於管道戳面積與周長之比．所以長和寬分別為A和B的矩形管道，其當量直徑對於任意截面形狀管道的當量直徑，都可按截面積的四倍和截面周長之比計算，因此，雷諾數的計算公式為，雷諾數小，意味著流體流動時各質點間的粘性力占主要地位，流體各質點平行於管路內壁有規則地流動，呈層流流動狀態。雷諾數大，意味著慣性力占主要地位，流體呈紊流流動狀態，一般管道雷諾數Re<2000為層流狀態，Re>4000為紊流狀態，Re=2000～4000為過渡狀態(這裡的過渡狀態是指流體的流動狀態是介與層流與湍流之間的一種中間狀態，而不同流體的從層流徹底轉變為湍流的雷諾數並不相同）。在不同的流動狀態下，流體的運動規律．流速的分布等都是不同的，因而管道內流體的平均流速υ與最大流速υmax的比值也是不同的。因此雷諾數的大小決定了粘性流體的流動特性。
雷諾數的流量表達式為：
M——被測介質的質量流量kg/h：
Q——被測介質的容積流量m/h；
D——管道內徑mm；
v——工作狀態下被測介質的動力粘度Pa·S
p——工作狀態下被測介質的運動粘度m2/s
式中的常數值，依式中各參數的單位不同而異。當採用非式中指定的單位時，常數值應作相應的修正。
管道雷諾數Rep與速度比V/Vmax的關係
試驗表明，外部條件幾何相似時(幾何相似的管子，
流體流過幾何相似的物體等)，若它們的雷諾數相等，則流體流動狀態也是幾何相似的(流體動力學相似)。這一相似規律正是流量測量節流裝置標準化的基礎。可見，雷諾數確切地反映了流體的流動特性是流量測量中常用的參數． / H: p! w+ Q6 L G
* H- T n9 c! d5 _# K7 L8 \$ d! l
雷諾數的流量表達式為： ! f) R5 g7 Q- y- g* H
" B* n8 b! M2 e: ]" I3 C# V
. `2 P0 o# Y1 c" b* \# ]
M——被測介質的質量流量kg/h： / ]8 }5 l+ H& S1 U' a" F9 M
Q——被測介質的容積流量m/h； ) f) a+ Z& d9 ~2 K
D——管道內徑mm；
( c7 z) p" _/ n
v——工作狀態下被測介質的動力粘度Pa·S $ }. k) v5 D5 h! H
, J/ [1 F* r; a
p——工作狀態下被測介質的運動粘度m2/s
* ]% o( f; ?3 r5 N5 e/ ^
式中的常數值，依式中各參數的單位不同而異。當採用非式中指定的單位時，常數值應作相應的修正。
在使用雷諾數時，應注意其對應的定型尺寸。一般在給出的雷諾數Re的右下角注以角碼，表明對應的定型尺寸。在節流裝置的標準中，對管道直徑D而言的雷諾數記作ReD，而對節流元件孔徑d而言的雷諾數記作Red，兩者的關係式為ReD=βRed，式中的β為分流元件的直徑比，即β=d/D，使用時應注意。9 }7 Q5 M9 j+ W2 m# R: w5 S+ n
