定義
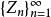零點收斂指數零點收斂指數(exponent of convergence of zeros)是量度函式零點稠密程度的一個量。設f(z)為一整函式，為其零點序列，則零點收斂指數λ=λ(0，f)定義為使得級數：
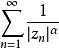零點收斂指數收斂的正數α所成的集合之最大下界。因此當α>λ時，級數收斂；當α<λ時，級數發散。若a為任一複數，{z}為f(z)-a的零點序列，即f(z)的a值點序列，則相應地可以定義f(z)的a值點序列的收斂指數λ(a，f)。
零點
設R為係數取自交換體K中的有理分式。稱K的元素α是R的零點，如果α可代入R中，且對應於R的有理函式在點α為零。這時R在點α的賦值是嚴格正的整數；稱之為零點α的重數。如果這個整數等於1，則稱α為單零點，否則稱α為多重零點。當R為多項式時，零點與根的概念是一致的。
設f為定義於開集D上的解析函式，而z為D的點。 則存在唯一的由自然數n與在z0的鄰域內解析的函式f所組成的偶(n，f)，使：f(z)=(z-z)nf(z)，其中f(z0)≠0. 如果n不等於零，則稱z0是f的零點。此時，整數n叫做z的重數。
解析函式
能局部展成冪級數的函式，它是複變函數論研究的主要對象。解析函式類包括了數學及其在自然科學和技術套用中所遇到的大多數函式，這類函式關於算術、代數和分析的各種基本運算是封閉的，解析函式在其自然存在的域中代表唯一的一個函式，因此，對解析函式的研究具有特殊的重要性。
對解析函式的系統研究開始於18世紀。歐拉在這方面做出許多貢獻。拉格朗日最早希望建立系統的解析函式理論，他曾試圖利用冪級數的工具來發展這種理論，但未獲成功。
法國數學家柯西以他自己的工作被公認為是解析函式理論的奠基者。1814年他定義正則函式為導數存在且連續，他批判了過去許多錯誤的結果，創立了若干法則，以保證級數運算的可靠性。1825年他得到了著名的柯西積分定理，隨後又建立了柯西積分公式。柯西利用這些工具得到了正則函式在它的定義域內處處可表為收斂的冪級數的結果，其逆命題亦真。所以解析和正則是等價的。後來黎曼對柯西的工作做出了重要的發展。1900年，法國數學家古爾薩改善了正則函式的定義，只要求函式在定義域中處處有導數。
外爾斯特拉斯以冪級數為出發點開展對解析函式的研究。他定義正則函式為可以展開為冪級數的函式，創立了解析開拓理論，並利用解析開拓定義完全解析函式。柯西的方法限於研究完全解析函式的所謂單值分支，必須通過解析開拓才能和外爾斯特拉斯的理論統一起來。
級數
級數是指將數列的項依次用加號連線起來的函式。典型的級數有正項級數、交錯級數、冪級數、傅立葉級數等。
級數理論是分析學的一個分支；它與另一個分支微積分學一起作為基礎知識和工具出現在其餘各分支中。二者共同以極限為基本工具，分別從離散與連續兩個方面，結合起來研究分析學的對象，即變數之間的依賴關係──函式。
零點收斂指數
零點收斂指數設a，a，a，…a，…為一個數列，稱a+a+…+a+…為一個級數。如果lim(a+a+…+a)存在，則稱無窮級數(簡稱級數)，(記為)收斂，並稱此極限值為級數的和。
級數不收斂，稱為發散。如果由級數各項的絕對值所構成的級數收斂，則原級數收斂，並稱原級數絕對收斂。不絕對收斂的收斂級數，稱為條件收斂級數；改變條件收斂級數中項的順序(更序)，就可能變成一個發散級數。
自從阿基米德以來，用分割求和的樸素思想解決求積問題時，在數量計算上，就總是以級數形式出現的。
17世紀中葉以來，級數收斂的概念逐步明確，從而有力地促進了微積分學基本概念——定積分的形成。級數在分析學中具有很重要的地位。利用級數，可以解超越方程、微分方程；或求定積分與超越函式的值等，它甚至還是某些函式的惟一表達式。
