障礙項

制約函式F(x,σ)=f(x)+σp(x)中的σp(x)稱為障礙項。障礙項的作用是在極小化過程中迫使疊代點靠近可行域，從而得到原問題的近似解。而且σ越大，近似程度越好。

障礙函式

(barrier function)

障礙函式亦稱內懲罰函式、圍牆函式或碰壁函式，是一類制約函式。

在數學領域約束最佳化中，障礙函式是一個連續函式，其中點的值隨著點到達最佳化問題的可行區域的邊界而增加到無窮大。這些函式用於通過更容易處理的目標函式中的懲罰項來代替不等式約束。

障礙函式F[x,σ]由目標函式f(x)和障礙項σp(x)構成，即F[x,σ]=f(x)+σp(x)。

定義

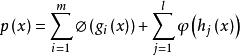障礙項

制約函式F(x,σ)=f(x)+σp(x)中的σp(x)稱為障礙項，其中 ，φ和ψ是滿足下述條件的連續函式：

當y≥0時，∅(y)=0；

當y<0時，∅(y)>0；

當y=0時，ψ(y)=0；

當y≠0時，ψ(y)>0。

作用

根據p(x)的定義，當x為可行點時p(x)=0，從而有F(x,σ)=f(x)；而當x不是可行點時，p(x)>0，σp(x)是一個很大的正數。它的存在是對點x偏離可行域的一種懲罰。

障礙項的作用是在極小化過程中迫使疊代點靠近可行域，從而得到原問題的近似解。而且σ越大，近似程度越好。