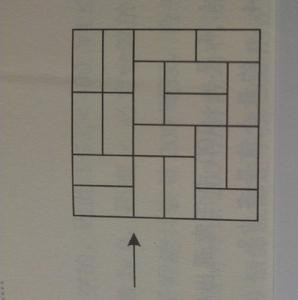
鋪磚問題
即是針對一個特定的道路，比如1*N的道路，有兩種磚塊來鋪設，一種是方磚1*1的，一種是長磚1*2的，用這兩種磚，有什麼鋪設方案？
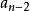鋪磚問題
鋪磚問題
鋪磚問題
鋪磚問題解決方案，就是採取遞推關係。假設方案數為，以最後一塊磚的種類為分析對象，如果是方磚，則方案數為；如果是長磚，則方案數為。那么總體的方案數。
求得遞推關係以後，根據齊次線性方程組的特徵方程，可以求得鋪磚方案數。
以上是最簡單的鋪磚問題，也是從數學的角度解釋什麼是鋪磚問題以及鋪磚問題的求解。
編程求解
鋪磚問題，其實還是一個動態規劃的問題，而且是一個狀態壓縮的動態規劃問題。所謂狀態壓縮型動態規劃，就是將不方便轉移或數據量極大的狀態用01字串來表示，這樣就可以方便的轉移狀態，同時節省了大量的空間。
有一個長H，寬W的廣場，要鋪滿2x1規格的磚塊，不允許磚塊重疊，求一共有多少種方案？（H，W均不超過11）
題目的數據範圍相當小，不過還沒有小到可以用DFS解決的規模（DFS每次只能把方案數增加1,而W=10,H=11的方案數為已經超過10^11了）。注意到題目的磚塊只有兩種擺放方式：橫著或者豎著。加之廣場邊長小於11,因此考慮用狀態壓縮動態規劃。用一個整數的每一位對應一個橫排每個位置是否有磚塊。
那么，轉移方程就是：F[i][S] = Sigma{F[i-1][S']} (S'可以轉移到S)
邊界是：F[1][0] = 1
需要找出各個狀態之間的轉移關係。這時DFS就派上用場了，我們只需考慮兩行，枚舉第一行的狀態i，根據i搜尋得到第二行能達到的狀態j，把adj[i][j]賦值為1.具體實現請看後面的程式。
獲得矩陣adj後，就可以用三個for逐行求出F[i][S]的方案了，最後輸出F[H+1][0].(即能將第h行鋪滿的方案數）.
此外，由於磚塊的面積是2，如果廣場面積是奇數，顯然是無解的，可以直接輸出0.
