概述
在基本代數中,配方法是一種用來把二次多項式化為一個一次多項式的平方與一個常數的和的方法。這種方法是把以下形式的多項式
化為
以上表達式中的係數a、b、c、d和e本身也可以是表達式,可以含有除x以外的變數。
配方法通常用來推導出二次方程的求根公式:
我們的目的是要把方程的左邊化為完全平方。由於問題中的完全平方具有(x + y) = x + 2xy + y的形式,可推出2xy = (b/a)x,因此y = b/2a。等式兩邊加上y = (b/2a),可得:
這個表達式稱為二次方程的求根公式。
幾何學的觀點
考慮把以下的方程配方:
方程的配方是在方程的兩邊同時加上一次項係數的一半的平方,而函式是在加上一次項係數一半的平方後再減去一次項係數一半的平方
對於任意的a、b(這裡的a、b可以代指任意一個式子,即包括超越式和代數式),都有
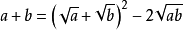 配方法
配方法,
(一般情況下,前一個公式最好用於對x²±y²配方,後一個公式最好用於對x²±ax進行配方)
對於任意的a、b、c,都有
 配方法
配方法(一般情況下,這個公式最好用於對x²+y²+z²進行配方)
配方時,只需要明確要進行配方兩項或三項,再套用上述公式即可。
解方程
在一元二次方程中,配方法其實就是把一元二次方程移項之後,在等號兩邊都加上一次項係數絕對值一半的平方。
【例】解方程:2x²+6x+6=4
分析:原方程可整理為:x²+3x+3=2,通過配方可得(x+1.5)²=0.5通過開方即可求解。
解:2x²+6x+6=4
<=>(x+1.5)²=1.25
x+1.5=1.25的平方根
求最值
【例】已知實數x,y滿足x²+3x+y-3=0,則x+y的最大值為____。
分析:將y用含x的式子來表示,再代入(x+y)求值。
解:x²+3x+y-3=0<=>y=3-3x-x²,
代入(x+y)得x+y=3-2x-x²=-(x²+2x-3)=-[(x+1)²-4]=4-(x+1)²。
由於(x+1)²≥0,故4-(x+1)²≤4.故推測(x+y)的最大值為4,此時x,y有解,故(x+y)的最大值為4.
證明非負性
【例】證明:a²+2b+b²-2c+c²-6a+11≥0
解:a²+2b+b²-2c+c²-6a+11=(a-3)²+(b+1)²+(c-1)²,結論顯然成立。
例分解因式x²-4x-12
解:x²-4x-12=x²-4x+4-4-12
=(x-2)²-16
=(x -6)(x+2)
求拋物線的頂點坐標
【例】求拋物線y=3x²+6x-3的頂點坐標。
解:y=3(x²+2x-1)=3(x²+2x+1-1-1)=3(x+1)²-6
所以這條拋物線的頂點坐標為(-1,-6)