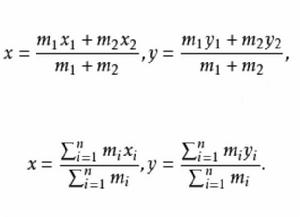基本介紹
質點系重心坐標是確定質點系重心位置的計算公式,在點P(x,y),P(x,y)上分別放置質量是m,m的兩個質點,它們的重心G的坐標為
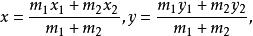 質點系重心坐標
質點系重心坐標一般地,在點P(x,y),P(x,y),…,P(x,y)上分別放置質量是m,m,…,m的n個質點,它們的重心G的坐標為
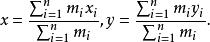 質點系重心坐標
質點系重心坐標相關分析
平行力系的中心
對一個存在合力的平行力系,如果平行力系中的每一個力都繞自身的作用點向同一個方向轉動一個相同的角度.仍然保持平行,則顯然合力也將轉動同一個角度,並且可以得出在進行上述轉動時,平行力系的合力作用線總是通過同一點,該點是合力的作用點,稱為 平行力系的中心。下面進行簡單證明。
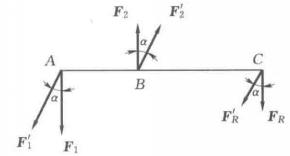 圖1
圖1假設上圖所示剛體的A、B的兩點上分別作用有反向、平行、大小不等的力 F₁和 F₂,F₁>F₂,由主矩為零的條件,可以確定主矢 F的作用點在AB連線的外分點C,作用線與 F₁和 F₂平行,即F₁·CE=F₂·CB。若兩力同時繞作用點向同一方向轉α角度變成 F'₁和 F'₂,則 F'₁和 F'₂的合力 F'也肯定通過點C,也向同一方向轉α角度。由於α是任意的.故C即為力系( F₁, F₂)的中心。對於其他存在合力的平行力系,也可以證明此結論是正確的。
由以上證明可知,當平行力系中各平行力繞其作用點向同一方向轉同一角度時,該平行力系合力作用線通過同一點,也就是該平行力系的中心。反過來說,某一平行力系的中心只與該平行力系中各力的大小和作用點位置有關,而與該平行力系的方向無關。具體確定某存在合力的平行力系的中心時,可以運用求合力作用位置的方法,確定平行力系中心的位置。
對於由集中力組成的平行力系,可由
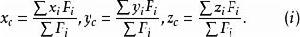 質點系重心坐標
質點系重心坐標求出其中心坐標。
質點系的重心及質心
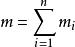 質點系重心坐標
質點系重心坐標如圖2所示,置於地球表面附近的由n個質點組成的質點系,第i個質點的質量為m,質點系總質量為 ,該質點所受重力為w,各質點上所受重力嚴格考慮的話並不平行。但是,一般工程上研究的質點系統的尺寸遠小於地球半徑,故這些力之間的夾角非常微小,所以各質點繫上所受力可以看成是鉛直向下的空間同向平行力系,其合力W就是整個質點系所受的重力,其大小為
 質點系重心坐標
質點系重心坐標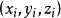 質點系重心坐標
質點系重心坐標當質點系中各質點空間位置確定時,合力W的作用線必定通過某一確定點C,這一點就稱為質點系的 重心。可以看出,置於地球表面附近的質點系的重心就是對應平行力系的中心,建立直角坐標系.假定第i個質點的坐標為 ,利用式(i)可得質點系的重心坐標為
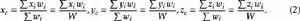 質點系重心坐標
質點系重心坐標質心就是所研究物體或物體系統質量的中心,其只與質點系的質量分布有關,與質點系是否受力無關。在研究質點系受外力作用發生運動狀態改變時,要用到質量的中心,即質心的概念。
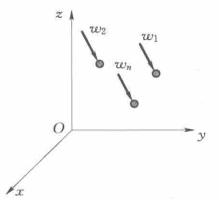 圖2(a)
圖2(a)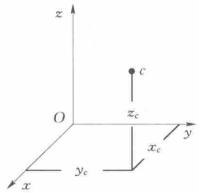 圖2(c)
圖2(c) 質點系重心坐標
質點系重心坐標在中學已學過, ,將這兩式代入式(2),化簡可得
 質點系重心坐標
質點系重心坐標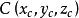 質點系重心坐標
質點系重心坐標由公式確定的 點定義為前述質點系的質心。
從式(3)中可以看出,質心只與質點系中質量的分布有關,不涉及重力,利用式(3)可以求質點系質心的位置。
質點系中各質點的質量是定值時,質點系的重心及質心取決於質點系中各質點的相對位置。當質點系中各質點的相對位置不發生變化時,質點系的重心及質心不會發生變化;當質點系中各質點的相對位置發生變化時,質點系的重心及質心隨著會發生相應的變化。