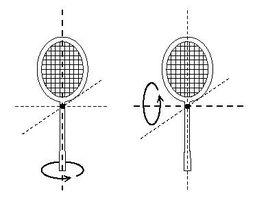
定理簡介
該效應最初是在1985年由俄羅斯太空人弗拉基米爾·賈尼別科夫(Vladimir Dzhanibekov)在空間站中偶然發現的,因此也被稱作賈尼別科夫效應(Dzhanibekov effect)。1991年,一篇公開發表的文章解釋了該效應。
定理實驗
在下面這個實驗中就能觀察到此效應:用手握住一個網球拍的拍柄,使其中一個拍面(記為A面)朝上並水平,然後用力向上拋起網球拍,讓網球拍繞水平面上垂直於拍柄的軸旋轉一個周期,並重新抓住拍柄,實驗順利的話你將會發現,原本朝上的A面也繞拍柄軸旋轉了大約半個周期後朝下了。如果你將拍面垂直於水平面拋起並接住,或者讓網球拍繞拍柄軸旋轉則不能看到類似的現象。
這個實驗可以用任何一個擁有三個轉動慣量不同的主軸的物體來完成,例如一本書或一個遙控器。該效應只需要物體的旋轉軸與其第二主軸稍有偏差,與空氣阻力或重力無關。
定理分析
網球拍定理可以藉助歐拉方程(Euler's equations)來定性分析。在不受外加轉矩的作用下,物體在轉動時遵循以下規律:
I1 · dω1/ dt = ( I2- I3) ω2 ω3(1)
I2 · dω2/ dt = ( I3- I1) ω3 ω1(2)
I3 · dω3/ dt = ( I1- I2) ω1 ω2(3)
其中 I1, I2, I3為物體主軸方向上的轉動慣量,假定 I1> I2> I3。物體主軸方向上的角速度分量為別為 ω1, ω2, ω3,它們對時間的導數,即角加速度分別為 dω1/ dt, dω2/ dt, dω3/ dt。
我們首先考慮物體繞其第一主軸 I1旋轉的情況。自然條件(非理想條件)下,物體的旋轉軸不可能完全與第一主軸平行,因此我們假定在另外兩個主軸上有微小的角速度分量。由公式(1)可知, dω1/ dt小到可以忽略。再對公式(2)兩邊求導,求出 dω3/ dt來替換公式(3)中的 dω3/ dt,整理可得:
I2 I3 · dω2/( dt)= ( I3- I1)( I1- I2)( ω1) ω2
dω2/( dt)= (負值)× ω2
我們注意到的變化 ω2符合簡諧運動( ω3同理)。因此,物體繞第一主軸旋轉時是穩定的。同理,物體繞第三主軸旋轉也可以得出相同的公式,即物體繞第三主軸旋轉時也是穩定的。
但是當物體繞第二主軸旋轉時情況就不一樣了。這一次是 dω2/ dt小到可以忽略。同樣的,我們用公式(1)求出 dω3/ dt來替換公式(3)中的 dω3/ dt,整理可得:
I1 I3 · dω1/( dt)= ( I2- I3)( I1- I2)( ω2) ω1
dω1/( dt)= (正值)× ω1
這次我們注意到 ω1是在增加的( ω3同理),這就說明物體繞第二主軸旋轉時是不穩定的。所以只要物體的旋轉軸與第二主軸稍有偏差,物體就會在旋轉時發生快速翻轉的現象。