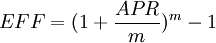計算公式
例如,假如存款按6%的年度百分率(APR)每月計複利,也就是說,存款每月按規定的APR的1/12獲得利息,這時,真正的利息率實際上是0.5%月利率(用小數表示是每月0.005)。我們發現,實際年利率(EFF)可以用年初每美元到年末的終值計算。在該例中我們算得:
FV=1.00512 =1.0616778(美元)
實際年利率等於該數減1:
EFF=1.0616778-1=0.0616778或每年6.616778%
實際年利率的總計算公式為
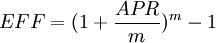 計息次數
計息次數其中,APR為年度百分率;m為每年計息次數。下表所列的是6%的年度百分率在不同計息次數下的實際利率。
| 計息次數 | m | 實際年利率(%) |
| 一年一次 | 1 | 6.00000 |
| 半年一次 | 2 | 6.09000 |
| 一季度一次 | 4 | 6.13614 |
| 一月一次 | 12 | 6.16778 |
| 一周一次 | 52 | 6.17998 |
| 一天一次 | 365 | 6.18313 |
| 連續計息 | 無窮 | 6.18365 |
率假如一年計息一次,那么實際年利率就等於年度百分率。隨著計息次數的增加,實際年利率會變得越來越大並趨向於一個極限。當m趨向於無窮大時,(1 + APR / m)m 會越來越趨近於eAPR ,其中e為2.71828(約到小數點後第五位)。在該例中,e0.06 = 1.0618364。所以,當連續計複利時,EFF=0.0618365或每年6.18365%。