定義
公元1858年，莫比烏斯發現：把一個扭轉180°後再兩頭粘接起來的紙條，具有魔術般的性質。
因為，普通紙帶具有兩個面（即雙側曲面），一個正面，一個反面，兩個面可以塗成不同的顏色；而這樣的紙帶只有一個面（即單側曲面），一隻小蟲可以爬遍整個曲面而不必跨過它的邊緣！
我們把這種由莫比烏斯發現的神奇的單面紙帶，稱為莫比烏斯環帶。
實例
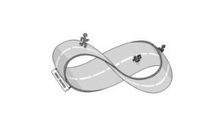莫比烏斯環帶拿一張白的長紙條，把一面塗成黑色，然後把其中一端翻一個身，
如同右圖那樣粘成一個莫比烏斯帶。現在像圖中那樣用剪刀沿紙帶的中央把它剪開。你就會驚奇地發現，紙帶不僅沒有一分為二，反而像圖中那樣剪出一個兩倍長的紙圈！
有趣的是：新得到的這個較長的紙圈，本身卻是一個雙側曲面，它的兩條邊界自身雖不打結，但卻相互套在一起！為了讓讀者直觀地看到這一不太容易想像出來的事實，我們可以把上述紙圈，再一次沿中線剪開，這回可真的一分為二了！得到的是兩條互相套著的紙圈，而原先的兩條邊界，則分別包含於兩條紙圈之中，只是每條紙圈本身並不打結罷了。
比如旋轉三個半圈的帶子再剪開後會形成一個三葉結。剪開帶子之後再進行旋轉，然後重新貼上則會變成數個莫比烏斯帶。
莫比烏斯帶常被認為是無窮大符號「∞」的創意來源，因為如果某個人站在一個巨大的莫比烏斯帶的表面上沿著他能看到的“路”一直走下去，他就永遠不會停下來。但是這是一個不真實的傳聞，因為「∞」的發明比莫比烏斯帶還要早。
莫比烏斯帶還有更為奇異的特性。一些在平面上無法解決的問題，卻不可思議地在莫比烏斯帶上獲得了解決！
比如在普通空間無法實現的“手套易位問題：人左右兩手的手套雖然極為相像，但卻有著本質的不同。我們不可能把左手的手套貼切地戴到右手上去；也不能把右手的手套貼切地戴到左手上來。無論你怎么扭來轉去，左手套永遠是左手套，右手套也永遠是右手套！不過，倘若自你把它搬到莫比烏斯帶上來，那么解決起來就易如反掌了。”
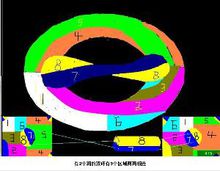莫比烏斯環帶在自然界有許多物體也類似於手套那樣，
它們本身具備完全相像的對稱部分，但一個是左手系的，另一個是右手系的，它們之間有著極大的不同。
右圖是一個管子旋轉180度連線，中間一根管子旋轉90度安裝在兩頭，就是一個虧格為2時8個區域兩兩相連。林格爾（G.Ringel）和楊斯（F.YOUNGS）1974年證明：Np=[(7+√1+48P)/2],P=2時，N2=8。就是右圖。
