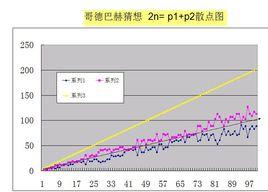
自然數集的結構特點
把自然數定義為等差數列AN,再把兩個AN重組為2n的新集合CN,那么它就變成了,1,1,2,2,3,3,4,4,5,5,6,6。。。。,那么它的通項公式是什麼,CN的公式如下:
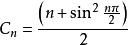 自然數密碼
自然數密碼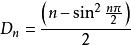 自然數密碼
自然數密碼如果CN 再把0 加入到數列之首,又變成同樣的變種DN集合0,1,1,2,2,3,3,4,4,5,5,6,6。。。。DN集合的通項公式是:把CN與DN 通項相加就等於AN
套用
把數集3,5,7,9,11,。。。。。加2Cn結果為:5.7,11,13,17,19,25.。。。。結果是素數及偽素數的集合pn,它的通項公式為
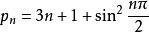 自然數密碼
自然數密碼求pn中以5為因子的組合數,那么這時的n取值公式又是什麼,結果如下
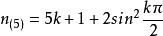 自然數密碼
自然數密碼如此我們就得到了偽素數及素數的通項公式了
通過以上方程可以求出偽素數變數n的通項公式,用三維變數來表示它N(X,Y),x,y均正整數
n 為偶數時
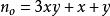 自然數密碼
自然數密碼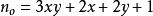 自然數密碼
自然數密碼n 為奇數時
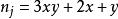 自然數密碼
自然數密碼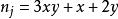 自然數密碼
自然數密碼偽素數變數N(X,Y)也僅僅為正整數。。。而素數變數就是非N(X,Y)的n才是。。。。可見偽素數及素數是個三維度變數。。。。。。。
全體素數倒數函式
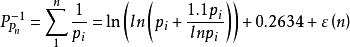 自然數密碼
自然數密碼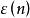 自然數密碼
自然數密碼是個震盪函式如下圖:
 自然數密碼
自然數密碼n小的時候除2 以外基本較平,隨著n加大,曲線會上揚,在pn=31 附近誤差在-0.02左右,在pn=5072863附近誤差在0.0174168左右,局部是微震盪的,此公式比較接近函式的實際值。。。
全體自然倒數和
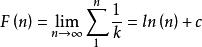 自然數密碼
自然數密碼c≈0.577215664901532860606512090082402431042159335,這就是 歐拉 -馬歇羅尼常數,但是實際中我們並不能達到極限狀態,對於有限區間如何取值,我們就需要對函式解碼,以下是自然數倒數在有限範圍內的解碼函式。。
全體自然倒數和解碼逼近函式
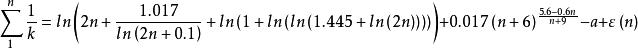 自然數密碼
自然數密碼a=0.115939501064126, ε(n)為余函式
解碼函式比原函式偏大,函式在n=1 時誤差為-0.0441205416846531,n(2,9)時誤差為0.0166525111249827~0.000175768034325063,n>=10時誤差為-0.000169478025731529左右,n特別大時逐漸時趨於0。誤差就是余函式ε(n)的取值。以下是ε(n)的圖像
 自然數密碼
自然數密碼全體奇數及偶數倒數和
通過初等函式的麥克勞林級數的展開式我們得到
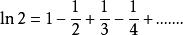 自然數密碼
自然數密碼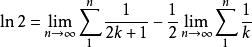 自然數密碼
自然數密碼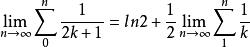 自然數密碼
自然數密碼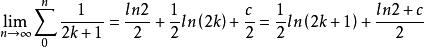 自然數密碼
自然數密碼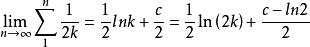 自然數密碼
自然數密碼同理得
由此得到
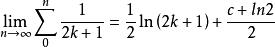 自然數密碼
自然數密碼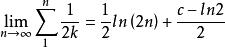 自然數密碼
自然數密碼c為歐拉 -馬歇羅尼常數,這就是通常的自然數倒數和問題,可見偶數的倒數小於它的平方根的對數,而奇數的倒數和大於它的平方根的對數
n的階乘問題
由於階乘函式增速過大,我們採用n比n的階乘的幾何平均值來描述它。我們採用的同樣是函式逼近法來解碼它,以下是它的解碼逼近函式公式
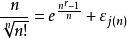 自然數密碼
自然數密碼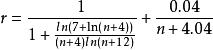 自然數密碼
自然數密碼 自然數密碼
自然數密碼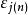 自然數密碼
自然數密碼左圖是余函式圖像
通過以上公式,大數階乘可以通過對數來計算它的值。。。。。 上式可以近似地改寫為以下公式:
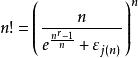 自然數密碼
自然數密碼逼近函式在2~9區間誤差最大在-0.11~-0.85之間,14~57區間解碼函式小於原函式誤差在0.0000813415266884832~0.00620524426495761,在58以後誤差為最大值為-0.00480492422863588對應 於n=212, 其他均小於此值。。。函式僅僅在14~57區間偏小於原函式,其他區間均偏大於原函式。。。誤差即ε(n)函式值。。。
素數分布及解碼
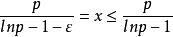 自然數密碼
自然數密碼素數分布具有一定規律,但是它的分布規律就是沒有相同點,我們即便是找到一些局部的規律性,但是它依然不能套用到全部,在尋找規律時,我們一般都採用函式逼近法去解碼,但是即便是解碼成功,它的余函式一樣不可以描述它。以下是素數分布的逼近函式:
以下是余函式圖
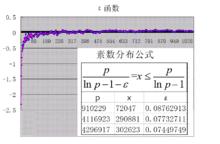 自然數密碼
自然數密碼以上解碼函式是821641以內所有素數歸納出來的,隨著素數的增加,逼近函式可能還會有一些微小的變動。這是目前最為接近的中值逼近解碼函式。余函式是素數分布的本身,是無法描述的,但是我們通過解碼,了解到它具有波動性和周期性。。。。。
素性檢測與哥德巴赫猜想的強證明
 自然數密碼
自然數密碼 自然數密碼
自然數密碼 自然數密碼
自然數密碼 自然數密碼
自然數密碼 自然數密碼
自然數密碼 自然數密碼
自然數密碼 自然數密碼
自然數密碼哥德巴赫散點圖
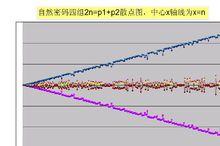 自然數密碼
自然數密碼 自然數密碼
自然數密碼偶數分解程式excel vba 函式代碼
REP(2n, i) 與2n- REP(2n, i)是邊際數除外的第i組方程解。RP(2N),與2n-RP(2N)為邊際第一組,多數是 2n=p1+1隻有部分為真得素數組,pr(2n)與2n-pr(2n)為邊際第二組,pzr(2n)與2n-pzr(2n)為中心素數組, PFR(2N)與2n-PFR(2N)是中心第二組素數組。散點圖如上圖。函式可以分解950萬內偶數,所有素數均在x=n 的x軸線上相交,所有n為非素數時均不與x=n 的x軸線相交,素數點pi到pi+1之間是數字黑洞。以上右圖為多組散點圖,左圖為四組散點圖。通解函式是REP(2n, i)。
Function REP(N As Variant, i As Variant) As Variant
Dim d As Variant
Dim a As Variant
Dim s As Variant
a = 0.5 * (N / 2 + 0.5 * (1 - (-1) ^ (N / 2)))
d = N - 1
If qp(d) > 0 Then
d = N - 1
Else
d = N - 3
End If
If d - 2 * i >= PZr(N) + 2 Then
d = d - 2 * i
Else
d = PZr(N): GoTo DD
End If
d = d
If a > 1 Then
s = 0
bb:
If qp(d) > 0 And qp(N - d) > 0 Then
s = s: d = d: GoTo DD
Else
s = s + 1
If d - 2 * s >= PZr(N) + 2 Then
d = d - 2 * s: GoTo bb
Else
d = PZr(N): GoTo DD
End If
End If
aa:
If s <= a + 1 Then
If qp(d) > 0 And qp(N - d) > 0 Then
d = d: GoTo DD
Else
d = d - 2: GoTo bb
End If
End If
End If
DD:
REP = d
End Function
Function PFr(N As Variant) As Variant
Dim d As Variant
Dim a As Variant
Dim s As Variant
a = 0.5 * (N / 2 + 0.5 * (1 - (-1) ^ (N / 2)))
d = PZr(N) + 2
If N - d >= 3 Then
d = d
Else
d = d - 2
End If
d = d
If qp(d) > 0 And qp(N - d) > 0 Then
d = d: GoTo DD
Else
If qp(d + 2) > 0 And qp(N - d - 2) > 0 Then
d = d + 2: GoTo DD
Else
If qp(d + 4) > 0 And qp(N - d - 4) > 0 Then
d = d + 4: GoTo DD
Else
d = d - 2
End If
End If
End If
d = d
If a > 1 Then
s = 0
bb:
If qp(d) > 0 And qp(N - d) > 0 Then
s = s: d = d: GoTo aa
Else
s = s + 1: d = K + 2 * s: GoTo bb
End If
aa:
If s <= a + 1 Then
If qp(N - d) > 0 Then
d = d: GoTo cc
Else
d = d + 2: GoTo bb
End If
End If
End If
cc:
d = d
If N - d = 1 And N = 4 Then
d = 2
End If
If N - d > 1 And N > 4 Then
d = d: GoTo DD
Else
d = d + 2: GoTo bb
End If
DD:
If N = 4 Then
PFr = 2
Else
PFr = d
End If
End Function
Function RP(N As Variant) As Variant
Dim d As Variant
Dim a As Variant
Dim s As Variant
Dim i As Variant
y = N - 1
a = 0.5 * (N / 2 + 0.5 * (1 - (-1) ^ (N / 2)))
d = N - 1
If qp(d) > 0 Then
d = N - 1
Else
d = N - 3
End If
If a > 1 Then
s = 0
bb:
If qp(d) > 0 Then
s = s: d = d: GoTo aa
Else
s = s + 1: d = N - 1 - 2 * s: GoTo bb
End If
aa:
If s <= a + 1 Then
If qp(N - d) > 0 Then
d = d: GoTo cc
Else
d = d - 2: GoTo bb
End If
End If
End If
cc:
RP = d
End Function
Function Pr(N As Variant) As Variant
Dim d As Variant
Dim a As Variant
Dim s As Variant
Dim i As Variant
y = N - 1
a = 0.5 * (N / 2 + 0.5 * (1 - (-1) ^ (N / 2)))
d = N - 1
If qp(d) > 0 Then
d = N - 1
Else
d = N - 3
End If
If a > 1 Then
s = 0
bb:
If qp(d) > 0 Then
s = s: d = d: GoTo aa
Else
s = s + 1: d = N - 1 - 2 * s: GoTo bb
End If
aa:
If s <= a + 1 Then
If qp(N - d) > 0 Then
d = d: GoTo cc
Else
d = d - 2: GoTo bb
End If
End If
End If
cc:
d = d
If N - d = 1 And N = 4 Then
d = 2: GoTo DD
End If
If N - d > 1 And N > 4 Then
d = d: GoTo DD
Else
d = d - 2: GoTo bb
End If
DD:
Pr = d
End Function
Function PZr(N As Variant) As Variant
Dim d As Variant
Dim a As Variant
Dim s As Variant
If (-1) ^ (N / 2) = -1 Then
K = N / 2
Else
K = (N / 2) + 1
End If
a = 0.5 * (N / 2 + 0.5 * (1 - (-1) ^ (N / 2)))
d = K
If qp(d) > 0 And qp(N - d) > 0 Then
d = K: GoTo DD
Else
d = K + 2
End If
d = d
If a > 1 Then
s = 0
bb:
If qp(d) > 0 And qp(N - d) > 0 Then
s = s: d = d: GoTo aa
Else
s = s + 1: d = K + 2 * s: GoTo bb
End If
aa:
If s <= a + 1 Then
If qp(N - d) > 0 Then
d = d: GoTo cc
Else
d = d + 2: GoTo bb
End If
End If
End If
cc:
d = d
If N - d = 1 And N = 4 Then
d = 2
End If
If N - d > 1 And N > 4 Then
d = d: GoTo DD
Else
d = d + 2: GoTo bb
End If
DD:
If N = 4 Then
PZr = 2
Else
PZr = d
End If
End Function
Function p(m As Variant, W As Variant) As Variant
If W >= m Then
p = 1
End If
If m / W = Int(m / W) And W < m Then
p = 0
Else
p = 1
End If
End Function
Function qp(m As Variant) As Variant
Dim sy As Long
Dim s As Long, s1 As Long, s2 As Long, s3 As Long, s4 As Long, s5 As Long, s6 As Long
Dim s7 As Long, s8 As Long, s9 As Long, s10 As Long, s11 As Long, s12 As Long, s13 As Long
Dim s14 As Long, s15 As Long, s16 As Long, s17 As Long, s18 As Long, s19 As Long
Dim s20 As Long, s21 As Long, s22 As Long, s23 As Long, s24 As Long, s25 As Long
Dim s26 As Long, s27 As Long, s28 As Long, s29 As Long, s30 As Long, s31 As Long
s0 = p(m, 3) * p(m, 5) * p(m, 7) * p(m, 11) * p(m, 13) * p(m, 17) * p(m, 19) * p(m, 23) * p(m, 29) * p(m, 31) * p(m, 37)
s = p(m, 3) * p(m, 5) * p(m, 7) * p(m, 11) * p(m, 13) * p(m, 17) * p(m, 19) * p(m, 23) * p(m, 29) * p(m, 31) * p(m, 37) * p(m, 41) * p(m, 43) * p(m, 47) * p(m, 53) * p(m, 59) * p(m, 61) * p(m, 67) * p(m, 71) * p(m, 73) * p(m, 79) * p(m, 83) * p(m, 89) * p(m, 97)
s1 = p(m, 101) * p(m, 103) * p(m, 107) * p(m, 109) * p(m, 113) * p(m, 127) * p(m, 131) * p(m, 137) * p(m, 139) * p(m, 149) * p(m, 151) * p(m, 157) * p(m, 163) * p(m, 167) * p(m, 173) * p(m, 179) * p(m, 181) * p(m, 191)
s2 = p(m, 193) * p(m, 197) * p(m, 199) * p(m, 211) * p(m, 223) * p(m, 227) * p(m, 229) * p(m, 233) * p(m, 239) * p(m, 241) * p(m, 251) * p(m, 257) * p(m, 263) * p(m, 269) * p(m, 271) * p(m, 277) * p(m, 281) * p(m, 283)
s3 = p(m, 293) * p(m, 307) * p(m, 311) * p(m, 313) * p(m, 317) * p(m, 331) * p(m, 337) * p(m, 347) * p(m, 349) * p(m, 353) * p(m, 359) * p(m, 367) * p(m, 373) * p(m, 379) * p(m, 383) * p(m, 389) * p(m, 397) * p(m, 401)
s4 = p(m, 409) * p(m, 419) * p(m, 421) * p(m, 431) * p(m, 433) * p(m, 439) * p(m, 443) * p(m, 449) * p(m, 457) * p(m, 461) * p(m, 463) * p(m, 467) * p(m, 479) * p(m, 487) * p(m, 491) * p(m, 499) * p(m, 503) * p(m, 509)
s5 = p(m, 521) * p(m, 523) * p(m, 541) * p(m, 547) * p(m, 557) * p(m, 563) * p(m, 569) * p(m, 571) * p(m, 577) * p(m, 587) * p(m, 593) * p(m, 599) * p(m, 601) * p(m, 607) * p(m, 613) * p(m, 617) * p(m, 619) * p(m, 631)
s6 = p(m, 641) * p(m, 643) * p(m, 647) * p(m, 653) * p(m, 659) * p(m, 661) * p(m, 673) * p(m, 677) * p(m, 683) * p(m, 691) * p(m, 701) * p(m, 709) * p(m, 719) * p(m, 727) * p(m, 733) * p(m, 739) * p(m, 743) * p(m, 751)
s7 = p(m, 757) * p(m, 761) * p(m, 769) * p(m, 773) * p(m, 787) * p(m, 797) * p(m, 809) * p(m, 811) * p(m, 821) * p(m, 823) * p(m, 827) * p(m, 829) * p(m, 839) * p(m, 853) * p(m, 857) * p(m, 881) * p(m, 883) * p(m, 857)
s8 = p(m, 859) * p(m, 863) * p(m, 877) * p(m, 907) * p(m, 911) * p(m, 919) * p(m, 929) * p(m, 937) * p(m, 941) * p(m, 947) * p(m, 953) * p(m, 967) * p(m, 971) * p(m, 977) * p(m, 983) * p(m, 991) * p(m, 997) * p(m, 1009)
s9 = p(m, 1013) * p(m, 1019) * p(m, 1021) * p(m, 1031) * p(m, 1033) * p(m, 1039) * p(m, 1049) * p(m, 1051) * p(m, 1061) * p(m, 1063) * p(m, 1069) * p(m, 1087) * p(m, 1091) * p(m, 1093) * p(m, 1097) * p(m, 1103) * p(m, 1109)
s10 = p(m, 1303) * p(m, 1307) * p(m, 1217) * p(m, 1223) * p(m, 1117) * p(m, 1123) * p(m, 1129) * p(m, 1151) * p(m, 1153) * p(m, 1163) * p(m, 1171) * p(m, 1181) * p(m, 1187) * p(m, 1193) * p(m, 1201) * p(m, 1213) * p(m, 1229)
s11 = p(m, 1231) * p(m, 1237) * p(m, 1249) * p(m, 1259) * p(m, 1277) * p(m, 1279) * p(m, 1283) * p(m, 1289) * p(m, 1291) * p(m, 1297) * p(m, 1301) * p(m, 1319) * p(m, 1321) * p(m, 1327) * p(m, 1361) * p(m, 1367) * p(m, 1373)
s12 = p(m, 1381) * p(m, 1399) * p(m, 1409) * p(m, 1423) * p(m, 1427) * p(m, 1429) * p(m, 1433) * p(m, 1439) * p(m, 1447) * p(m, 1451) * p(m, 1453) * p(m, 1459) * p(m, 1471) * p(m, 1481) * p(m, 1483) * p(m, 1487) * p(m, 1489)
s13 = p(m, 1493) * p(m, 1499) * p(m, 1511) * p(m, 1523) * p(m, 1531) * p(m, 1543) * p(m, 1549) * p(m, 1553) * p(m, 1559) * p(m, 1567) * p(m, 1571) * p(m, 1579) * p(m, 1583) * p(m, 1597) * p(m, 1601) * p(m, 1607) * p(m, 1609)
s14 = p(m, 1613) * p(m, 1619) * p(m, 1621) * p(m, 1627) * p(m, 1637) * p(m, 1657) * p(m, 1663) * p(m, 1667) * p(m, 1669) * p(m, 1693) * p(m, 1697) * p(m, 1699) * p(m, 1709) * p(m, 1721) * p(m, 1723) * p(m, 1733) * p(m, 1741)
s15 = p(m, 1747) * p(m, 1753) * p(m, 1759) * p(m, 1777) * p(m, 1783) * p(m, 1787) * p(m, 1789) * p(m, 1801) * p(m, 1811) * p(m, 1823) * p(m, 1831) * p(m, 1847) * p(m, 1861) * p(m, 1867) * p(m, 1871) * p(m, 1873) * p(m, 1877)
s16 = p(m, 1879) * p(m, 1889) * p(m, 1901) * p(m, 1907) * p(m, 1913) * p(m, 1931) * p(m, 1933) * p(m, 1949) * p(m, 1951) * p(m, 1973) * p(m, 1979) * p(m, 1987) * p(m, 1993) * p(m, 1997) * p(m, 1999) * p(m, 2003) * p(m, 2011)
s17 = p(m, 2017) * p(m, 2027) * p(m, 2029) * p(m, 2039) * p(m, 2053) * p(m, 2063) * p(m, 2069) * p(m, 2081) * p(m, 2083) * p(m, 2087) * p(m, 2089) * p(m, 2099) * p(m, 2111) * p(m, 2113) * p(m, 2129) * p(m, 2131) * p(m, 2137)
s18 = p(m, 2141) * p(m, 2143) * p(m, 2153) * p(m, 2161) * p(m, 2179) * p(m, 2203) * p(m, 2207) * p(m, 2213) * p(m, 2221) * p(m, 2237) * p(m, 2239) * p(m, 2243) * p(m, 2251) * p(m, 2267) * p(m, 2269) * p(m, 2273) * p(m, 2281)
s19 = p(m, 2287) * p(m, 2293) * p(m, 2297) * p(m, 2309) * p(m, 2311) * p(m, 2333) * p(m, 2339) * p(m, 2341) * p(m, 2347) * p(m, 2351) * p(m, 2357) * p(m, 2371) * p(m, 2377) * p(m, 2381) * p(m, 2383) * p(m, 2389) * p(m, 2393)
s20 = p(m, 2399) * p(m, 2411) * p(m, 2417) * p(m, 2423) * p(m, 2437) * p(m, 2441) * p(m, 2447) * p(m, 2459) * p(m, 2467) * p(m, 2473) * p(m, 2477) * p(m, 2503) * p(m, 2521) * p(m, 2531) * p(m, 2539) * p(m, 2543) * p(m, 2549)
s21 = p(m, 2551) * p(m, 2557) * p(m, 2579) * p(m, 2591) * p(m, 2593) * p(m, 2609) * p(m, 2617) * p(m, 2621) * p(m, 2633) * p(m, 2647) * p(m, 2657) * p(m, 2659) * p(m, 2663) * p(m, 2671) * p(m, 2677) * p(m, 2683) * p(m, 2687)
s22 = p(m, 2689) * p(m, 2693) * p(m, 2699) * p(m, 2707) * p(m, 2711) * p(m, 2713) * p(m, 2719) * p(m, 2729) * p(m, 2731) * p(m, 2741) * p(m, 2749) * p(m, 2753) * p(m, 2767) * p(m, 2777) * p(m, 2789) * p(m, 2791) * p(m, 2797)
s23 = p(m, 2801) * p(m, 2803) * p(m, 2819) * p(m, 2833) * p(m, 2837) * p(m, 2843) * p(m, 2851) * p(m, 2857) * p(m, 2861) * p(m, 2879) * p(m, 2887) * p(m, 2897) * p(m, 2903) * p(m, 2909) * p(m, 2917) * p(m, 2927) * p(m, 2939)
s24 = p(m, 2953) * p(m, 2957) * p(m, 2963) * p(m, 2969) * p(m, 2971) * p(m, 2999) * p(m, 3001) * p(m, 3011) * p(m, 3019) * p(m, 3023) * p(m, 3037) * p(m, 3041) * p(m, 3049) * p(m, 3061) * p(m, 3067) * p(m, 3079) * p(m, 3083)
If m <= 37 ^ 2 Then
sy = s0: GoTo hh
End If
If m <= 97 ^ 2 And m > 37 ^ 2 Then
sy = s: GoTo hh
End If
If m <= 191 ^ 2 And m > 97 ^ 2 Then
sy = s * s1: GoTo hh
End If
If m <= 283 ^ 2 And m > 191 ^ 2 Then
sy = s * s1 * s2: GoTo hh
End If
If m <= 401 ^ 2 And m > 283 ^ 2 Then
sy = s * s1 * s2 * s3: GoTo hh
End If
If m <= 509 ^ 2 And m > 401 ^ 2 Then
sy = s * s1 * s2 * s3 * s4: GoTo hh
End If
If m <= 631 ^ 2 And m > 509 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5: GoTo hh
End If
If m <= 751 ^ 2 And m > 631 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6: GoTo hh
End If
If m <= 857 ^ 2 And m > 751 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7: GoTo hh
End If
If m <= 1009 ^ 2 And m > 857 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8: GoTo hh
End If
If m <= 1109 ^ 2 And m > 1009 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9: GoTo hh
End If
If m <= 1229 ^ 2 And m > 1109 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10: GoTo hh
End If
If m <= 1373 ^ 2 And m > 1229 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11: GoTo hh
End If
If m <= 1489 ^ 2 And m > 1373 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12: GoTo hh
End If
If m <= 1609 ^ 2 And m > 1489 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13: GoTo hh
End If
If m <= 1741 ^ 2 And m > 1609 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14: GoTo hh
End If
If m <= 1877 ^ 2 And m > 1741 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15: GoTo hh
End If
If m <= 2011 ^ 2 And m > 1877 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16: GoTo hh
End If
If m <= 2137 ^ 2 And m > 2011 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17: GoTo hh
End If
If m <= 2281 ^ 2 And m > 2137 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18: GoTo hh
End If
If m <= 2393 ^ 2 And m > 2281 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18 * s19: GoTo hh
End If
If m <= 2549 ^ 2 And m > 2393 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18 * s19 * s20: GoTo hh
End If
If m <= 2687 ^ 2 And m > 2549 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18 * s19 * s20 * s21: GoTo hh
End If
If m <= 2797 ^ 2 And m > 2687 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18 * s19 * s20 * s21 * s22: GoTo hh
End If
If m <= 2939 ^ 2 And m > 2797 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18 * s19 * s20 * s21 * s22 * s23: GoTo hh
End If
If m <= 3083 ^ 2 And m > 2939 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18 * s19 * s20 * s21 * s22 * s23 * s24: GoTo hh
End If
hh:
sy = sy
If m = 2 Then
sy = 1
End If
If m / 2 - Int(m / 2) = 0 And m > 2 Then
sy = 0
Else
sy = sy
End If
sy = sy
qp = sy
End Function
偶數分解程式AUTOCAD vba 函式代碼
 自然數密碼
自然數密碼散點矩陣圖
本程式比素數篩選更加困難,計算時間更長,所以i變數要分段取值,否則會造成電腦當機現象。。。。
Sub 偶數分解()
Dim t As Variant
Dim co As Variant
Dim s As Variant
Dim pointObj As AcadPoint
Dim location(0 To 2) As Double
Dim p(4 To 40000) As Double
Dim i As Variant
Dim J As Variant
s = 0
For i = 402 To 500 Step 2
If i = 4 Then
t = 1
Else
t = 0.5 * (i / 2 + 0.5 * (1 - (-1) ^ (i / 2)))
End If
For J = 0 To t Step 1
location(0) = 15 * i: location(1) = 30 * (i / 2 - REP(i, J)): location(2) = 0#
s = s + 1
Set pointObj = ThisDrawing.ModelSpace.AddPoint(location)
pointObj.color = acGreen
location(0) = 15 * i: location(1) = 30 * REP(i, J) - 15 * i: location(2) = 0#
s = s
Set pointObj = ThisDrawing.ModelSpace.AddPoint(location)
pointObj.color = acBlue
Next J
Next i
MsgBox "合計" & s & "組素數!"
End Sub
Function REP(N As Variant, i As Variant) As Variant
Dim d As Variant
Dim a As Variant
Dim s As Variant
a = 0.5 * (N / 2 + 0.5 * (1 - (-1) ^ (N / 2)))
d = N - 1
If qp(d) > 0 Then
d = N - 1
Else
d = N - 3
End If
If d - 2 * i >= PZr(N) + 2 Then
d = d - 2 * i
Else
d = PZr(N): GoTo DD
End If
d = d
If a > 1 Then
s = 0
bb:
If qp(d) > 0 And qp(N - d) > 0 Then
s = s: d = d: GoTo DD
Else
s = s + 1
If d - 2 * s >= PZr(N) + 2 Then
d = d - 2 * s: GoTo bb
Else
d = PZr(N): GoTo DD
End If
End If
aa:
If s <= a + 1 Then
If qp(d) > 0 And qp(N - d) > 0 Then
d = d: GoTo DD
Else
d = d - 2: GoTo bb
End If
End If
End If
DD:
REP = d
End Function
Function PZr(N As Variant) As Variant
Dim d As Variant
Dim a As Variant
Dim s As Variant
If (-1) ^ (N / 2) = -1 Then
k = N / 2
Else
k = (N / 2) + 1
End If
a = 0.5 * (N / 2 + 0.5 * (1 - (-1) ^ (N / 2)))
d = k
If qp(d) > 0 And qp(N - d) > 0 Then
d = k: GoTo DD
Else
d = k + 2
End If
d = d
If a > 1 Then
s = 0
bb:
If qp(d) > 0 And qp(N - d) > 0 Then
s = s: d = d: GoTo aa
Else
s = s + 1: d = k + 2 * s: GoTo bb
End If
aa:
If s <= a + 1 Then
If qp(N - d) > 0 Then
d = d: GoTo cc
Else
d = d + 2: GoTo bb
End If
End If
End If
cc:
d = d
If N - d = 1 And N = 4 Then
d = 2
End If
If N - d > 1 And N > 4 Then
d = d: GoTo DD
Else
d = d + 2: GoTo bb
End If
DD:
If N = 4 Then
PZr = 2
Else
PZr = d
End If
End Function
Function p(m As Variant, W As Variant) As Variant
If W >= m Then
p = 1
End If
If m / W = Int(m / W) And W < m Then
p = 0
Else
p = 1
End If
End Function
Function qp(m As Variant) As Variant
Dim sy As Long
Dim s As Long, s1 As Long, s2 As Long, s3 As Long, s4 As Long, s5 As Long, s6 As Long
Dim s7 As Long, s8 As Long, s9 As Long, s10 As Long, s11 As Long, s12 As Long, s13 As Long
Dim s14 As Long, s15 As Long, s16 As Long, s17 As Long, s18 As Long, s19 As Long
Dim s20 As Long, s21 As Long, s22 As Long, s23 As Long, s24 As Long, s25 As Long
Dim s26 As Long, s27 As Long, s28 As Long, s29 As Long, s30 As Long, s31 As Long
s0 = p(m, 3) * p(m, 5) * p(m, 7) * p(m, 11) * p(m, 13) * p(m, 17) * p(m, 19) * p(m, 23) * p(m, 29) * p(m, 31) * p(m, 37)
s = p(m, 3) * p(m, 5) * p(m, 7) * p(m, 11) * p(m, 13) * p(m, 17) * p(m, 19) * p(m, 23) * p(m, 29) * p(m, 31) * p(m, 37) * p(m, 41) * p(m, 43) * p(m, 47) * p(m, 53) * p(m, 59) * p(m, 61) * p(m, 67) * p(m, 71) * p(m, 73) * p(m, 79) * p(m, 83) * p(m, 89) * p(m, 97)
s1 = p(m, 101) * p(m, 103) * p(m, 107) * p(m, 109) * p(m, 113) * p(m, 127) * p(m, 131) * p(m, 137) * p(m, 139) * p(m, 149) * p(m, 151) * p(m, 157) * p(m, 163) * p(m, 167) * p(m, 173) * p(m, 179) * p(m, 181) * p(m, 191)
s2 = p(m, 193) * p(m, 197) * p(m, 199) * p(m, 211) * p(m, 223) * p(m, 227) * p(m, 229) * p(m, 233) * p(m, 239) * p(m, 241) * p(m, 251) * p(m, 257) * p(m, 263) * p(m, 269) * p(m, 271) * p(m, 277) * p(m, 281) * p(m, 283)
s3 = p(m, 293) * p(m, 307) * p(m, 311) * p(m, 313) * p(m, 317) * p(m, 331) * p(m, 337) * p(m, 347) * p(m, 349) * p(m, 353) * p(m, 359) * p(m, 367) * p(m, 373) * p(m, 379) * p(m, 383) * p(m, 389) * p(m, 397) * p(m, 401)
s4 = p(m, 409) * p(m, 419) * p(m, 421) * p(m, 431) * p(m, 433) * p(m, 439) * p(m, 443) * p(m, 449) * p(m, 457) * p(m, 461) * p(m, 463) * p(m, 467) * p(m, 479) * p(m, 487) * p(m, 491) * p(m, 499) * p(m, 503) * p(m, 509)
s5 = p(m, 521) * p(m, 523) * p(m, 541) * p(m, 547) * p(m, 557) * p(m, 563) * p(m, 569) * p(m, 571) * p(m, 577) * p(m, 587) * p(m, 593) * p(m, 599) * p(m, 601) * p(m, 607) * p(m, 613) * p(m, 617) * p(m, 619) * p(m, 631)
s6 = p(m, 641) * p(m, 643) * p(m, 647) * p(m, 653) * p(m, 659) * p(m, 661) * p(m, 673) * p(m, 677) * p(m, 683) * p(m, 691) * p(m, 701) * p(m, 709) * p(m, 719) * p(m, 727) * p(m, 733) * p(m, 739) * p(m, 743) * p(m, 751)
s7 = p(m, 757) * p(m, 761) * p(m, 769) * p(m, 773) * p(m, 787) * p(m, 797) * p(m, 809) * p(m, 811) * p(m, 821) * p(m, 823) * p(m, 827) * p(m, 829) * p(m, 839) * p(m, 853) * p(m, 857) * p(m, 881) * p(m, 883) * p(m, 857)
s8 = p(m, 859) * p(m, 863) * p(m, 877) * p(m, 907) * p(m, 911) * p(m, 919) * p(m, 929) * p(m, 937) * p(m, 941) * p(m, 947) * p(m, 953) * p(m, 967) * p(m, 971) * p(m, 977) * p(m, 983) * p(m, 991) * p(m, 997) * p(m, 1009)
s9 = p(m, 1013) * p(m, 1019) * p(m, 1021) * p(m, 1031) * p(m, 1033) * p(m, 1039) * p(m, 1049) * p(m, 1051) * p(m, 1061) * p(m, 1063) * p(m, 1069) * p(m, 1087) * p(m, 1091) * p(m, 1093) * p(m, 1097) * p(m, 1103) * p(m, 1109)
s10 = p(m, 1303) * p(m, 1307) * p(m, 1217) * p(m, 1223) * p(m, 1117) * p(m, 1123) * p(m, 1129) * p(m, 1151) * p(m, 1153) * p(m, 1163) * p(m, 1171) * p(m, 1181) * p(m, 1187) * p(m, 1193) * p(m, 1201) * p(m, 1213) * p(m, 1229)
s11 = p(m, 1231) * p(m, 1237) * p(m, 1249) * p(m, 1259) * p(m, 1277) * p(m, 1279) * p(m, 1283) * p(m, 1289) * p(m, 1291) * p(m, 1297) * p(m, 1301) * p(m, 1319) * p(m, 1321) * p(m, 1327) * p(m, 1361) * p(m, 1367) * p(m, 1373)
s12 = p(m, 1381) * p(m, 1399) * p(m, 1409) * p(m, 1423) * p(m, 1427) * p(m, 1429) * p(m, 1433) * p(m, 1439) * p(m, 1447) * p(m, 1451) * p(m, 1453) * p(m, 1459) * p(m, 1471) * p(m, 1481) * p(m, 1483) * p(m, 1487) * p(m, 1489)
s13 = p(m, 1493) * p(m, 1499) * p(m, 1511) * p(m, 1523) * p(m, 1531) * p(m, 1543) * p(m, 1549) * p(m, 1553) * p(m, 1559) * p(m, 1567) * p(m, 1571) * p(m, 1579) * p(m, 1583) * p(m, 1597) * p(m, 1601) * p(m, 1607) * p(m, 1609)
s14 = p(m, 1613) * p(m, 1619) * p(m, 1621) * p(m, 1627) * p(m, 1637) * p(m, 1657) * p(m, 1663) * p(m, 1667) * p(m, 1669) * p(m, 1693) * p(m, 1697) * p(m, 1699) * p(m, 1709) * p(m, 1721) * p(m, 1723) * p(m, 1733) * p(m, 1741)
s15 = p(m, 1747) * p(m, 1753) * p(m, 1759) * p(m, 1777) * p(m, 1783) * p(m, 1787) * p(m, 1789) * p(m, 1801) * p(m, 1811) * p(m, 1823) * p(m, 1831) * p(m, 1847) * p(m, 1861) * p(m, 1867) * p(m, 1871) * p(m, 1873) * p(m, 1877)
s16 = p(m, 1879) * p(m, 1889) * p(m, 1901) * p(m, 1907) * p(m, 1913) * p(m, 1931) * p(m, 1933) * p(m, 1949) * p(m, 1951) * p(m, 1973) * p(m, 1979) * p(m, 1987) * p(m, 1993) * p(m, 1997) * p(m, 1999) * p(m, 2003) * p(m, 2011)
s17 = p(m, 2017) * p(m, 2027) * p(m, 2029) * p(m, 2039) * p(m, 2053) * p(m, 2063) * p(m, 2069) * p(m, 2081) * p(m, 2083) * p(m, 2087) * p(m, 2089) * p(m, 2099) * p(m, 2111) * p(m, 2113) * p(m, 2129) * p(m, 2131) * p(m, 2137)
s18 = p(m, 2141) * p(m, 2143) * p(m, 2153) * p(m, 2161) * p(m, 2179) * p(m, 2203) * p(m, 2207) * p(m, 2213) * p(m, 2221) * p(m, 2237) * p(m, 2239) * p(m, 2243) * p(m, 2251) * p(m, 2267) * p(m, 2269) * p(m, 2273) * p(m, 2281)
s19 = p(m, 2287) * p(m, 2293) * p(m, 2297) * p(m, 2309) * p(m, 2311) * p(m, 2333) * p(m, 2339) * p(m, 2341) * p(m, 2347) * p(m, 2351) * p(m, 2357) * p(m, 2371) * p(m, 2377) * p(m, 2381) * p(m, 2383) * p(m, 2389) * p(m, 2393)
s20 = p(m, 2399) * p(m, 2411) * p(m, 2417) * p(m, 2423) * p(m, 2437) * p(m, 2441) * p(m, 2447) * p(m, 2459) * p(m, 2467) * p(m, 2473) * p(m, 2477) * p(m, 2503) * p(m, 2521) * p(m, 2531) * p(m, 2539) * p(m, 2543) * p(m, 2549)
s21 = p(m, 2551) * p(m, 2557) * p(m, 2579) * p(m, 2591) * p(m, 2593) * p(m, 2609) * p(m, 2617) * p(m, 2621) * p(m, 2633) * p(m, 2647) * p(m, 2657) * p(m, 2659) * p(m, 2663) * p(m, 2671) * p(m, 2677) * p(m, 2683) * p(m, 2687)
s22 = p(m, 2689) * p(m, 2693) * p(m, 2699) * p(m, 2707) * p(m, 2711) * p(m, 2713) * p(m, 2719) * p(m, 2729) * p(m, 2731) * p(m, 2741) * p(m, 2749) * p(m, 2753) * p(m, 2767) * p(m, 2777) * p(m, 2789) * p(m, 2791) * p(m, 2797)
s23 = p(m, 2801) * p(m, 2803) * p(m, 2819) * p(m, 2833) * p(m, 2837) * p(m, 2843) * p(m, 2851) * p(m, 2857) * p(m, 2861) * p(m, 2879) * p(m, 2887) * p(m, 2897) * p(m, 2903) * p(m, 2909) * p(m, 2917) * p(m, 2927) * p(m, 2939)
s24 = p(m, 2953) * p(m, 2957) * p(m, 2963) * p(m, 2969) * p(m, 2971) * p(m, 2999) * p(m, 3001) * p(m, 3011) * p(m, 3019) * p(m, 3023) * p(m, 3037) * p(m, 3041) * p(m, 3049) * p(m, 3061) * p(m, 3067) * p(m, 3079) * p(m, 3083)
If m <= 37 ^ 2 Then
sy = s0: GoTo hh
End If
If m <= 97 ^ 2 And m > 37 ^ 2 Then
sy = s: GoTo hh
End If
If m <= 191 ^ 2 And m > 97 ^ 2 Then
sy = s * s1: GoTo hh
End If
If m <= 283 ^ 2 And m > 191 ^ 2 Then
sy = s * s1 * s2: GoTo hh
End If
If m <= 401 ^ 2 And m > 283 ^ 2 Then
sy = s * s1 * s2 * s3: GoTo hh
End If
If m <= 509 ^ 2 And m > 401 ^ 2 Then
sy = s * s1 * s2 * s3 * s4: GoTo hh
End If
If m <= 631 ^ 2 And m > 509 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5: GoTo hh
End If
If m <= 751 ^ 2 And m > 631 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6: GoTo hh
End If
If m <= 857 ^ 2 And m > 751 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7: GoTo hh
End If
If m <= 1009 ^ 2 And m > 857 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8: GoTo hh
End If
If m <= 1109 ^ 2 And m > 1009 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9: GoTo hh
End If
If m <= 1229 ^ 2 And m > 1109 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10: GoTo hh
End If
If m <= 1373 ^ 2 And m > 1229 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11: GoTo hh
End If
If m <= 1489 ^ 2 And m > 1373 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12: GoTo hh
End If
If m <= 1609 ^ 2 And m > 1489 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13: GoTo hh
End If
If m <= 1741 ^ 2 And m > 1609 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14: GoTo hh
End If
If m <= 1877 ^ 2 And m > 1741 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15: GoTo hh
End If
If m <= 2011 ^ 2 And m > 1877 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16: GoTo hh
End If
If m <= 2137 ^ 2 And m > 2011 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17: GoTo hh
End If
If m <= 2281 ^ 2 And m > 2137 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18: GoTo hh
End If
If m <= 2393 ^ 2 And m > 2281 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18 * s19: GoTo hh
End If
If m <= 2549 ^ 2 And m > 2393 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18 * s19 * s20: GoTo hh
End If
If m <= 2687 ^ 2 And m > 2549 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18 * s19 * s20 * s21: GoTo hh
End If
If m <= 2797 ^ 2 And m > 2687 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18 * s19 * s20 * s21 * s22: GoTo hh
End If
If m <= 2939 ^ 2 And m > 2797 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18 * s19 * s20 * s21 * s22 * s23: GoTo hh
End If
If m <= 3083 ^ 2 And m > 2939 ^ 2 Then
sy = s * s1 * s2 * s3 * s4 * s5 * s6 * s7 * s8 * s9 * s10 * s11 * s12 * s13 * s14 * s15 * s16 * s17 * s18 * s19 * s20 * s21 * s22 * s23 * s24: GoTo hh
End If
hh:
sy = sy
If m = 2 Then
sy = 1
End If
If m / 2 - Int(m / 2) = 0 And m > 2 Then
sy = 0
Else
sy = sy
End If
sy = sy
qp = sy
End Function