簡介
羅曼-梅尼紹夫定理是一個關於函式在區域內的解析性的判定定理。此定理由羅曼(Looman,H.)1923年給出較廣的定理，但他的證明有缺陷。1933年，梅尼紹夫改正了羅曼的缺陷。於是，這個定理稱為羅曼-梅尼紹夫定理。
定理
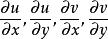羅曼-梅尼紹夫定理 設f(z)=u+iv在區域D內有定義，u和v在D內連續，最多除去D的可數個點外， 存在，且在D內除去一個勒貝格測度為零的集合外，柯西-黎曼方程成立，則f=u+iv在D內全純。
發展
柯西(Cauchy,A.-L.)最初於1814年給出解析函式的定理時，要求導函式的連續性，從而推出柯西定理。
1900年，古爾薩(Goursat,E.-J.-B.)在沒有導數連續性的假定下證明了柯西定理。人們期望與柯西解析函式的定義相等價的定義，即用柯西-黎曼方程定義的解析性能有相應的改進。
1923年，羅曼(Looman,H.)給出了上述更廣的定理，但他的證明有缺陷。
1933年，梅尼紹夫改正了羅曼的缺陷。於是，這個定理稱為羅曼-梅尼紹夫定理。
