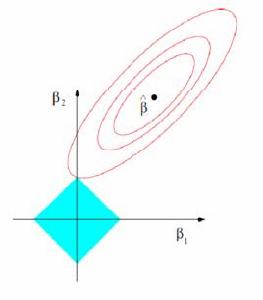
基本思想
把非線性約束最佳化問題轉化為無線性最佳化約束問題。依據如何將目標函式和約束函式進行組合,人們導出了許多不同形式的罰函式。由於這些早期方法均需要求解一系列無約束的罰函式極小化問題,故通常稱之為序列無約束極小化方法(Sequential Unconstrained Minimization Technique),簡稱SUMT。
基本思路:通過引進一個乘法因子把約束條件連線到目標函式上,從而將有約束的最最佳化問題轉化為無約束條件的問題。合理的罰函式可以在當搜尋到不可行點時,是目標函式值變得很大,離約束條件越遠懲罰越大。
分類
外罰函式法
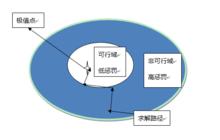 外罰函式法
外罰函式法 根據約束的特點,構造某種懲罰函式,然後加到目標函式中去,將約束問題求解轉化為一系列的無約束問題。這種“懲罰策略”,對於無約束問題求解過程中的那些企圖違反約束條件的目標點給予懲罰。如右圖:
通過上述方法,我們可以把有約束的問題化為無約束問題求解。也就是所謂的外罰函式法。
但是外罰函式的原理主要是套用了近似最優並且近似可行的,近似最優可以接受,但是近似可行在實際運用中讓人無法接受。這一點可以由內罰函式解決。
內罰函式法
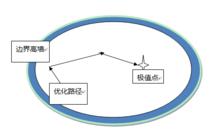 內罰函式法
內罰函式法 相比於外罰函式法在不可行區域加懲罰,內罰函式法在可行域邊界築起高牆,讓目標函式無法穿過,就把目標函式擋在可行域內了。
但是這種懲罰策略只適用於不等式約束問題,並要求可行域的內點集非空,否則,每個可行點都是邊界點,都加上無窮大懲罰,懲罰也就失去意義了。
優缺點對比
1)由於無約束最最佳化問題的解法目前已有許多很有效的算法,如DFP,BFGS等,所以在求解複雜得多的約束最佳化問題是,工程技術人員一般會採用罰函式法——SUMT外點法和內點法。
2)內點法適用於解含不等式約束問題,並且每次疊代的點都是可行點,這是設計人員所希望的。但要求初始點為可行域的內點,需要相當的工作量,同時它不能處理等式約束;外點法適於解既含等式約束又含不等式約束的最佳化問題,初始點可以是可行域之外的點,卻不能保證近似最優解是可行的。
3)罰函式法對於增廣的目標函式的Hessian矩陣的條件數隨罰因子增大或減小而增大,造成在求解無約束最最佳化問題時的困難,如何選擇罰因子往往進退維谷。如外罰函式法,欲使得無約束問題接近於原約束問題,應該選擇儘可能大的罰因子;但為了減輕求解無約束問題的困難,又應選取較小的罰因子,否則增廣矩陣病態。這也是罰函式法的固有弱點。
懲罰因子
懲罰因子是用來權衡損失和分類間隔的權重,懲罰因子越大,表明重視損失,如果懲罰因子選取的非常大,那么如果有分錯的樣本,對其的懲罰非常大,將導致出現硬間隔的效果。不斷增大懲罰因子的值,總能實現將樣本點完全正確的分類,但是這樣將會導致過擬合,泛化能力不夠。
如果在同一個問題中,對不同的樣本點用不同的懲罰因子也是可以的。對給定正負樣本賦予不同的懲罰因子,這樣對於如果正負樣本點的數目差別比較大,可以對樣本數目比較小的樣本類別賦予較大的權重,否則此類樣本錯分的機率將增大。如果對於不同的樣本點賦予不同的懲罰因子,這樣從理論上來說,應該會有更好的分類效果,分別考慮每個樣本的懲罰因子,確定其對於錯分的影響,但是這樣對於複雜性又有所提高,需要單獨考慮每個樣本。但是對於樣本點比較少的時候,比較適合分別賦予權重,有更好的效果。
套用
電機最佳化設計
在電機最佳化設計中套用廣義罰函式法最佳化方法,既可以避免罰函式內點法因罰因子取得不當而造成的尋優困難,又保留了尋優逼近邊界的優點,通過目標函式調整和罰函式的容差疊代,可以達到快速收斂的目的。同時,廣義罰函式最佳化方法,還具有邊界附近進一步搜尋最優點的特性。在套用中,該方法是一種實用性很強而有效的內點尋優方法。
在機械領域,利用廣義罰函式最佳化方法編制的計算機尋優模組與各類外點法或可行方案尋求方法結合,具有顯著的最佳化效果。
廣義指數因子預測
選擇合適的罰函式和損失函式構建廣義指數因子預測模型,能夠比較準確地進行預測,其總體預測精度較高且較為穩定。該模型實施的關鍵在於預報方程的變數選擇和係數估計,線上性回歸模型的擬合過程中引入罰函式能夠壓縮回歸方程係數估計,將方程中一部分自變數的係數壓縮為0,從而達到自變數選擇、降低誤差方差的目的,並保證預報方程的穩定性,從而提高預測精度.因此,套用罰函式方法來實現廣義指數因子預報方程的擬合是合理的。