線性規劃模型
正文
一種特殊形式的數學規劃模型，即目標函式和約束條件是待求變數的線性函式、線性等式或線性不等式的數學規劃模型。它可用於解決各種領域內的極值問題。它所描述的典型問題是怎樣以最優的方式在各項活動中間分配有限資源的問題。任何一個線性規劃問題可以按下列方式表述：假設有м項有限的資源要在n項活動中間進行分配。給各項資源規定腳標1,2,…,м,給各項活動規定腳標1,2,…,n,設x j（即決策變數,有時亦稱控制變數）為j項活動的水平，j=1,2,…,n。決策變數x1,x2,…,x n的一組數值代表一個方案（或計畫）。設 z為選定的某個效益量度（總效益指標），它的數值衡量當採取一組活動水平（x1，x2，…，x n）時所得到的總效益。設c j為每一單位的x j所提供的效益。設 b j為i項資源在分配時可被利用的量，最後，設a ij（i=1,2,…,м；j=1,2,…,n）為i項資源被每單位j 項活動所消耗（或使用）的量。於是，將各項資源分配給各項活動以獲得最最佳化結果的規劃問題具有下列數學模型：
選擇x1，x2，…,x n的值，藉以使
z=c1x1+c2x2+……+c n x n達到最大，且滿足下列各項限制條件：
a11x1+ a12x2+……a1n x n≤b1
a21x1+ a22x2+……+a2n x n≤b2
a m1x1+a m2x2+……+amnxn≤bm
及 x1≥0，x2≥0，…，xn≥0
這個數學模型可以等價地表述為下列更為簡潔的矩陣形式：
選擇x的值，藉以使z=cTx達到最大，且滿足下列條件：
A X≤b
x≥0
式中
x =（x1,x2…,x n）T（n維列向量）
cT=（c1,c2,…c n）（n維行向量）
b=（b1,b2,…b m）T（m維列向量）
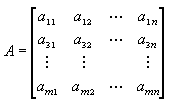（м×n矩陣）
線性規劃模型中z稱為目標函式，A x≤b和x≥0稱為約束條件；x是決策變數，A、b以及c稱為模型的參數。
以上是線性規劃模型的典型形式。
然而，在實際工作中，並不是所有的線性規劃問題都能表述為典型形式的數學模型，而可能出現下列情形：①使目標函式z達到最小，而不是使z達到最大；②約束條件組A x≤b被破壞,即其中有些約束條件是“≥”的不等式；③有些約束條件是等式；④非負性約束條件 x≥0被破壞。
在上述幾種情況下，只需將模型的有關部分加以改寫，便可使模型等價地變成典型形式。
