概念基礎——橢圓函式
簡介
橢圓函式也叫第一類橢圓函式，是第二、第三類橢圓函式的基本，雙周期亞純函式的統稱。在歷史上，橢圓函式是作為橢圓積分的反函式而引入的，故名。
設2ω，2ω'為橢圓函式 f(z) 的兩個基本周期，且
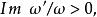第三類橢圓函式
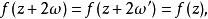第三類橢圓函式f(z) 在以任意一點 z 及 z+2ω，z+2ω+2ω'，z+2ω' 為頂點的平行四邊形（稱為周期平行四邊形）內極點的個數（n階極點算作n個極點）稱為橢圓函式 f(z) 的階。
橢圓函式的性質
橢圓函式具有下列性質：
1、若 f(z) 為橢圓函式，則其任意階導數 f(z) 也是橢圓函式，基本周期不變；
2、橢圓函式的階有限；
3、劉維爾第一定理：零階橢圓函式必為常數；
4、劉維爾第二定理：橢圓函式在任一周期平行四邊形內各極點處留數之和必為0；
因此，橢圓函式在任一周期平行四邊形內不可能只有一個（一階）極點。換言之，不存在一階橢圓函式。
5、橢圓函式在任一周期平行四邊形內零點的個數（n階零點算作n個零點）等於它的階；
6、劉維爾第三定理：對於任一常數C，方程 f(z)=C 在周期平行四邊形內根的個數（n重根算作n個根）等於 f(z) 的階；
7、劉維爾第四定理：在一個周期平行四邊形內，橢圓函式零點a(k=1,2,…)之和與極點b(k=1,2,…)之和相差某一周期，即
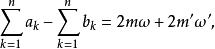第三類橢圓函式m，m'為整數。
最簡單的橢圓函式是二階橢圓函式。在這些函式中，或者把（在任一周期平行四邊形中）具有一個二階極點（留數為0）的函式選作標準函式（外爾斯特拉斯橢圓函式），或者把具有兩個一階極點（留數互相抵消）的函式選作標準函式（雅克比橢圓函式）。
第三類橢圓函式
第三類橢圓函式(elliptic function of the third kind )是橢圓函式的進一步推廣。如果亞純函式 f(u) 滿足
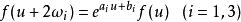第三類橢圓函式（ω 及 a，b 均為常數），則稱 f(u) 為第三類橢圓函式。外爾斯特拉斯σ函式就屬於第三類橢圓函式。
2ω及2ω仍稱為第三類橢圓函式的基本周期。
橢圓θ函式
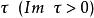第三類橢圓函式周期為 1 和 的第三類橢圓函式。定義為
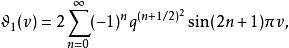第三類橢圓函式
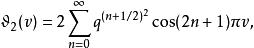第三類橢圓函式
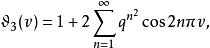第三類橢圓函式
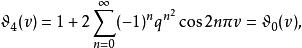第三類橢圓函式
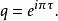第三類橢圓函式其中
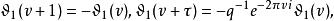第三類橢圓函式
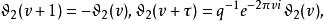第三類橢圓函式
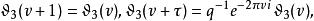第三類橢圓函式
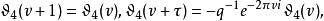第三類橢圓函式
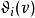第三類橢圓函式
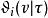第三類橢圓函式任何橢圓函式都可表示為幾個θ函式之商，有時還把 寫成以標明周期。
外爾斯特拉斯σ函式
一種第三類橢圓函式，定義為
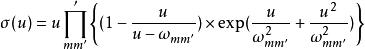第三類橢圓函式其中
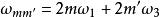第三類橢圓函式
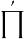第三類橢圓函式表示對一切整數m及m'求積，m=m'=0項除外。σ(u)具有擬周期性，即
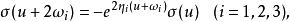第三類橢圓函式其中ω=-(ω+ω)，η=ζ(ω)，ζ(u)為外爾斯特拉斯ζ函式。
