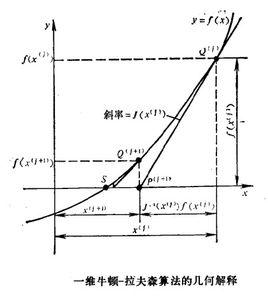
基本介紹
牛頓-拉夫森算法是對非線性方程作泰勒展開並取一次近似的結果。
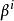 牛頓-拉夫森算法
牛頓-拉夫森算法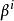 牛頓-拉夫森算法
牛頓-拉夫森算法在討論非線性最小二乘時,目標函式J(β)對β是非線性的, 如果是第i個疊代值,考慮在附近將J(β)展開成二次函式。令
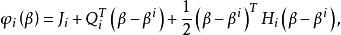 牛頓-拉夫森算法
牛頓-拉夫森算法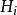 牛頓-拉夫森算法
牛頓-拉夫森算法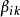 牛頓-拉夫森算法
牛頓-拉夫森算法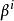 牛頓-拉夫森算法
牛頓-拉夫森算法其中是由J的二階導數組成的矩陣,它的第k行第l列的元素是(是的第k個分量):
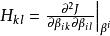 牛頓-拉夫森算法
牛頓-拉夫森算法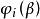 牛頓-拉夫森算法
牛頓-拉夫森算法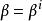 牛頓-拉夫森算法
牛頓-拉夫森算法是在附近對J的二階逼近。
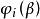 牛頓-拉夫森算法
牛頓-拉夫森算法現在來找出的穩定點,令
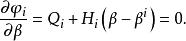 牛頓-拉夫森算法
牛頓-拉夫森算法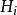 牛頓-拉夫森算法
牛頓-拉夫森算法如果是滿秩的,則有解
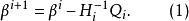 牛頓-拉夫森算法
牛頓-拉夫森算法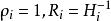 牛頓-拉夫森算法
牛頓-拉夫森算法用(1)作為第i次疊代所定義的算法稱為 牛頓-拉夫森算法,它相當於在一般的疊代格式中取。
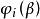 牛頓-拉夫森算法
牛頓-拉夫森算法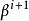 牛頓-拉夫森算法
牛頓-拉夫森算法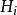 牛頓-拉夫森算法
牛頓-拉夫森算法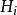 牛頓-拉夫森算法
牛頓-拉夫森算法如果J(β)是參數的二次函式(二次型),即J(β)與一致,則是J的穩定點,而且當是正定時它是一個最小值點。這時算法是可接受的,並且一次疊代就收斂。由於牛頓-拉夫森算法具有這種性質,所以稱它為二階收斂的,如果是負定的或不定的,則算法是不可接受的。
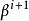 牛頓-拉夫森算法
牛頓-拉夫森算法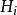 牛頓-拉夫森算法
牛頓-拉夫森算法當J不是二次型,一般與J的穩定點不一致,因此也就不可能一次疊代就收斂,但只要是正定的, 則算法是可接受的。
 牛頓-拉夫森算法
牛頓-拉夫森算法在實際套用時, 也可以在(1)中加上一個標量因子以加快其收斂速度, 即(1)修改為
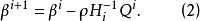 牛頓-拉夫森算法
牛頓-拉夫森算法適當選擇ρ>0即可取得較好的效果 。
牛頓-拉夫森方法的優缺點
牛頓-拉夫森方法有收斂快的優點,但是它也存在著缺點, 主要是H(β)的正定性不一定能得到保證,同時求H時需要計算二階導數這是很複雜的。為了克服這些困難,提出了各種改進方法。為了克服H的不定型問題提出了麥夸特(Marquardt)方法。為了克服求二階導數的困難提出高斯(Gauss)方法和變尺度方法 。