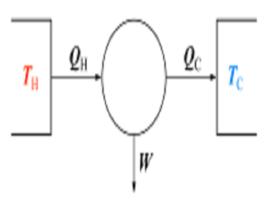
描述與解釋
| 名稱 | 符號 | 公式 | 自然變數 |
| 內能 |  熱動力勢能 熱動力勢能 | 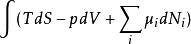 熱動力勢能 熱動力勢能 | 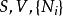 熱動力勢能 熱動力勢能 |
| 亥姆霍茲自由能 | 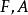 熱動力勢能 熱動力勢能 | 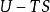 熱動力勢能 熱動力勢能 | 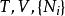 熱動力勢能 熱動力勢能 |
| 焓 |  熱動力勢能 熱動力勢能 | 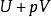 熱動力勢能 熱動力勢能 | 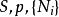 熱動力勢能 熱動力勢能 |
| 吉布斯能 |  熱動力勢能 熱動力勢能 | 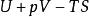 熱動力勢能 熱動力勢能 | 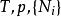 熱動力勢能 熱動力勢能 |
| 大勢能 | 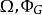 熱動力勢能 熱動力勢能 | 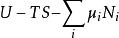 熱動力勢能 熱動力勢能 | 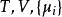 熱動力勢能 熱動力勢能 |
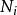 熱動力勢能
熱動力勢能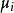 熱動力勢能
熱動力勢能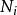 熱動力勢能
熱動力勢能T為溫度,S為熵,p為壓力,V為體積。荷目霍茲自由能通常以F表示,但是國際純粹與套用化學聯合會採用A來作為符號。 是系統里i型的粒子數, 是i型粒子的化學勢。為了保持完整性, 集合也包含了自然變數,雖然他們有時會被忽略。
這五種常見的位都是能量位(在英語中potential與potential energy有時會混用),不過他們也是熵位。熱動力方型圖可以用來找出你想要的勢能。
就像在機械力學中勢能被定義為作功的能力,不同的勢能有不同的意義。內能是作功的能力加上放熱的能力。吉布斯能是作非機械功的能力。焓是作非機械功的能力加上放熱的能力。亥姆霍茲自由能是作機械功加上非機械功的能力。從這些定義我們可以說ΔU是加到系統里的能量,ΔF是對系統作的總功,ΔG是對系統作的非機械功,ΔH是對系統作的非機械功加上給系統的熱。當要計算化學反應的平衡結果與測量化學反應時材料的性質時,熱動力位是非常有用的。化學反應通常在一些限制里發生,如定壓、定溫、定熵或定體積,這些條件成立時,有相應的熱動力勢能可以用來操作。如同機械力學,系統會趨向較低的勢能值並達成平衡。根據這些限制,勢能會達到一個不再變動的最小值。熱動力勢能可以用來估計在相應的限制中,熱動力系統中可用的總能量。
特例:
1)當一個封閉系統的熵與“外部參數”(如:體積)保持定值,在平衡時內能(U)會降低並達到最小值。這根據熱動力學第一與第二定律,也叫作最小能量原理,以下三行也是從此原理導出。
2)當一個封閉系統的溫度與外部參數保持定值,在平衡時荷姆霍茲自由能(F)會降低並達到最小值。
3)當一個封閉系統的壓力與外部參數保持定值,在平衡時焓(H)會降低並達到最小值。
4)當一個封閉系統的溫度、壓力與外部參數保持定值,在平衡時吉布斯能(G)會降低並達到最小值。
基礎方程
熱動力勢能的定義可能和熱動力學第一與第二定律有所差別,這組微分方程之前叫作基礎方程。 根據熱動力學第一定律,任何系統內能U的微分變數可以寫成進入系統的熱與系統對環境作的功與任何加入系統的新粒子的和。
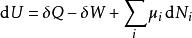 熱動力勢能
熱動力勢能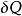 熱動力勢能
熱動力勢能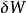 熱動力勢能
熱動力勢能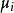 熱動力勢能
熱動力勢能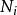 熱動力勢能
熱動力勢能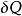 熱動力勢能
熱動力勢能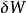 熱動力勢能
熱動力勢能這裡的 是流入系統的無限小的熱, 是系統作的無限小的功 是i粒子的化學位, 是i粒子的粒子數。(注意: 與 都不是恰當微分。所以這些變數的微小變化在此記為δ而不是 d。)
根據熱動力學第二定律,我們可以由狀態函式與它們的微分來表示內能的改變。如果發生在準靜態變化中,我們得到:
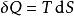 熱動力勢能
熱動力勢能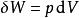 熱動力勢能
熱動力勢能這裡T是溫度,S是熵,p是壓力,V是體積。當是可逆過程時等號成立。
這領出了內能在準靜可逆變化中的標準微分形式:
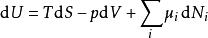 熱動力勢能
熱動力勢能由於U、S、V是狀態的熱動力函式,上述關係在任意非可逆變化中也成立。如果系統擁有更多的外部變數而不是只有體積可以改變,基礎熱動力關係即可推廣到:
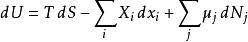 熱動力勢能
熱動力勢能 熱動力勢能
熱動力勢能 熱動力勢能
熱動力勢能這裡 是對應到外部變數 的廣義力。
多套用幾次勒讓德轉換,下列這四項勢能的微分關係也成立:
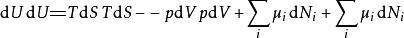 熱動力勢能
熱動力勢能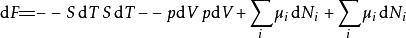 熱動力勢能
熱動力勢能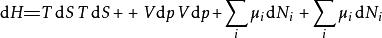 熱動力勢能
熱動力勢能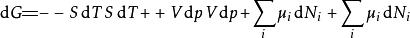 熱動力勢能
熱動力勢能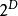 熱動力勢能
熱動力勢能注意上述每個等式右邊的無限小的量皆是等式左方的勢能的自然變數。類似的方程如系統的所有其他熱動力勢能可以被找出。這裡將有一個基礎方程為每個熱動力勢能造成總計為個基礎方程。