基本介紹
兩條線段的公度
 無公度線段
無公度線段 無公度線段
無公度線段 無公度線段
無公度線段取一個定長線段a,分別去量兩線段b、c,如果線段b、c都含有定長線段a的正整倍數而沒有剩餘,則線段a稱為線段b、c的公度。如圖1,,則線段a就是和的公度。
有公度的線段稱為可公度線段。
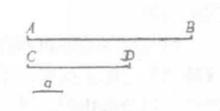 圖1
圖1不可公度線段
無公度線段亦稱“ 不可公度線段”,也說兩條輾轉相截永遠有剩餘的線段就是無公度線段。如,(1)正方形的一邊和對角線是無公度線段; (2)在一條直角邊是另一條直角邊二倍的直角三角形中,斜邊和直角邊是無公度線段;(3)底角為36°的等腰三角形的底和腰是無公度線段;(4)正三角形的邊和高是無公度線段 。
舉例說明
 無公度線段
無公度線段 無公度線段
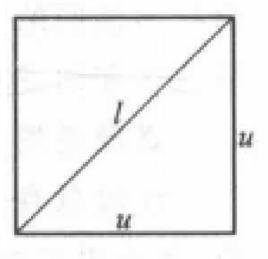
無公度線段定理 正方形的對角線和它的邊長是不可公度的,即是說的對角線不是一邊的有理數倍(圖2)。
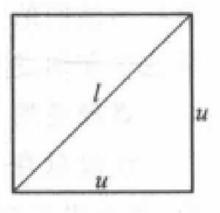 圖2
圖2我們用反證法證明,假設定理的反面成立,即假設
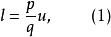 無公度線段
無公度線段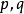 無公度線段
無公度線段其中代表整數,我們自然可以假設p和q是互素的,即沒有公因數,如果有,約去後就沒有公因數了。
式(1)可寫作
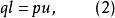 無公度線段
無公度線段式(2)平方得
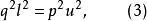 無公度線段
無公度線段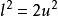 無公度線段
無公度線段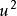 無公度線段
無公度線段由勾股定理,,代人式(3)並約去得
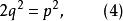 無公度線段
無公度線段式(4)左端能被2除盡,於是p只能是偶數,命
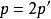 無公度線段
無公度線段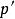 無公度線段
無公度線段其中表示整數,則
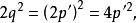 無公度線段
無公度線段即
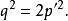 無公度線段
無公度線段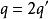 無公度線段
無公度線段仿上面得出q也必然是偶數:。
照此說來,若定理反面成立,p和q並非互素而有公因數2了,這矛盾反證了一個極為重要的事實:客觀空間中存在不可公度的量,正方形的對角線和邊就是不可公度的。
這一事實是被古希臘的哲學學派(畢達哥拉斯學派)發現的,並且給這個學派的哲學理論基礎帶來了巨大的衝擊。這個學派很重視數學,把數學概念作為他們哲學理論的基礎,他們認為“自然界的一切都可以度量,都受數的支配,一切事物的本質是數,……,在人的一切工作中,一切藝術、手藝和音樂中都可以看到數的本質和威力,數就是一切,事物的本質和基礎不是物質,而是數。”
這個觀點是唯心的。
正是把數(看作量與量之間的關係和度量的結果)作為自己哲學基礎的畢達哥拉斯學派發現了不可公度的線段存在,他們宣布“一切都可以度量”,自然意味著度量數是當時所理解的分數,而一邊等於單位的正方形的對角線卻沒有數的形式,這恰好與他們的哲學基礎“迎頭相撞”,於是他們感到驚訝,驚慌失措,禁止把無公度線段存在的發現泄露出去,但學派中一個成員泄露了秘密,被逐出學派。
真理是禁止不了的,無公度的線段存在這個事實傳開了,數學前進了一大步。線段總有個長度,即有個量數,正方形的對角線的量數,既不是整數,又不是分數,就超出當時所知道的數的範圍了。這種新認識的數被稱為無理數。相對而言,把原來認為僅有的數稱為 有理數。“無理”的並不是“無理數”,而是這個命名。無理數既不是整數和有限小數,也不是無限的循環小數,就必然是無限的不循環小數。這就是線段度量的第四種情況。
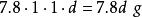 無公度線段
無公度線段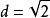 無公度線段
無公度線段不要以為度量線段才會出現無理數。例如說,鐵的比重是7.8 g/cm ,有一塊底面是每邊1cm的正方形,而高等於這個正方形的對角線d,重量就是;由於是無理數,這塊鐵的重量就是無理數。
這樣,人類在實踐中不斷發現,有所發明、創造和前進,把數的概念一步步擴大,由整數到分數,由正數到負數,由有理數到無理數,由實數到虛數,都是為實踐服務的 。