使用說明
下面介紹在實際工程中是如何運用滾球法的:由於使用避雷針做為接閃器時得到的保護範圍,一般具有較好的軸對稱性;而使用避雷帶等其它接閃器時所得到的保護範圍一般沒有軸對稱性,並且較為複雜,因此本文中只討論以避雷針做為接閃器的情況。
首先規定以下幾個條件:1、 滾球半徑為R(根據GB50057-2010可選30、45、60m)。
2、 地面無論坡度θ多大均為絕對平面。
3、 避雷針高度H指針尖豎直至地面的距離,針尖以下部分均視為接閃器。針桿均為豎直安裝,即避雷針與豎直軸重合。
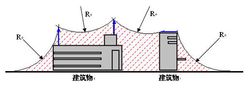 滾球法
滾球法一、 常規單針(θ=0, H=R)這種情況的保護範圍沿豎直軸具有完全軸對稱性,任選一個通過豎直軸的軸線剖面如下圖滾球球心的運動軌跡為:L(直線)+A(圓弧)+L(直線)註:A=π一個半徑為R的球沿θ=0的地面滾動,當它遇到高度H=R的避雷針時被阻礙,讓它翻過針尖繼續向前滾。滾球離開避雷針後我們即可看到滾球無法觸及的範圍就是滾球外圓運動軌跡的內包絡線與地面間的範圍。這就是該剖面上的保護範圍。由於保護範圍沿豎直軸具有完全軸對稱性,令該包絡線沿豎直軸鏇轉得到的實體就是實際空間的保護範圍。如果被保護的建築物完全在該實體的範圍內,則我們認為這樣的保護是有效的。
其他方法
而此時在具體工程套用中需要描述避雷針的保護範圍時僅給出一個保護半徑是遠不夠的!請看下面四種方法:
1、公式法方法:給出保護半徑的表達式(2)。優點:描述完整,精確。缺點:計算較複雜,不夠直觀。2、列r-β, h表方法:對方向β,高度h以一定的步長取值,帶入保護半徑的表達式(2)求出r列表即可。優點:描述精確。缺點:計算較複雜,不夠完整,不夠直觀。
3、校核危險剖面方法:根據經驗找出最有可能超出保護範圍的幾個危險點,然後做出通過這些危險點的軸線剖面進行校核即可。優點:計算簡單,精確。缺點:缺乏完整性及直觀性。
4、計算機輔助設計方法:使用三維繪圖軟體顯示計算結果。優點:非常完整,精確,直觀。缺點:計算較複雜。在四,五,六,七,八中,第1,2,4種方法存在計算較複雜的問題,都要上機編程計算。我們認為第3種方法較適用。
 滾球法
滾球法總結上述八種情況(一~八)。對坡度θ有變化的地形,或者安裝一隻以上的避雷針時,可以用以上八種情況組合而成進行分析,此時保護半徑的表達式會相當複雜。當使用我們推薦的第3種方法時,雖然需要一定的經驗,但是計算過程將變得簡單。通用的滾球法計算步驟一、 適用範圍說明 1、 任意形式的常規接閃器,包括避雷針,避雷帶,避雷線,避雷網。2、 接閃器的安裝數量不受限制。3、 地形起伏不受限制。4、 除保護對象外,其他建築物均視為大地。
二、 計算準備1、 選用空間三維直角坐標系{X,Y,Z}。X-Y平面為水平面,Z軸為豎直軸。2、確定地形邊界。被保護對象在X-Y平面上投影的外廓沿法線方向外移2R(滾球直徑)即可得到地形邊界的最小範圍。將地形邊界內的大地表面數位化,可得到一個面的集合,定義為集合A(2,0)。集合名稱註解:a、英文字母是集合的名稱。b、括弧中的第一位數字表示集合中的元素所形成的空間結構特性。1表示線結構,2表示面結構,3表示實體結構。c、括弧中的第二位數字每增加1就表示原集合中的元素經過1次運算又得到了一個新的集合。3、將被保護對象數位化,可得到一個實體的集合,定義為集合B(3,0)。4、將所設計的接閃器數位化,可得到一個線的集合,定義為集合C(1,0)
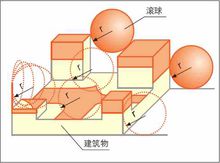 滾球法
滾球法三、 計算1、 最佳化大地表面。將A(2,0)通過最佳化計算得到A(2,1)。要求A(2,1)中任意一點的曲面半徑均不小於滾球半徑R。2、 將A(2,1)沿法線方向向上移動,距離為R,得到新的集合A(2,2)。3、 定義A(2,0) 與A(2,2)之間的空間為A(3,3)。4、 將C(1,0)沿法線方向向外擴大,距離為R,得到新的集合C(3,1)。5、 定義A(3,3) 與C(3,1)的並集為D(3,0)。6、 定義D(3,0) 的上表面為D(2,1)。7、 將D(2,1)沿法線方向向下移動,距離為R,得到新的集合D(2,2)。8、 定義A(2,1) 與D(2,2)之間的空間為E(3,0)。E(3,0)就是接閃器的保護範圍空間。9、 定義A(2,0) 與A(2,1)之間的空間為F(3,0)。F(3,0)是自然保護範圍空間。意思是不安裝接閃器該空間也受保護。10、 定義E(3,0) 與F(3,0)的並集為G(3,0)。G(3,0)就是總的保護範圍空間。11、 令H(3,0)=B(3,0)-B(3,0)∩G(3,0)。H(3,0)就是被保護對象上不在保護範圍內的空間。如果H(3,0)為空集,則表示被保護對象在接閃器的保護範圍內。
