泊松回歸模型
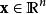 泊松回歸
泊松回歸代表由一組相互獨立的變數組成的向量,其泊松回歸的模型形式為:
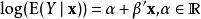 泊松回歸
泊松回歸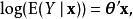 泊松回歸
泊松回歸亦可簡潔表示為:
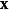 泊松回歸
泊松回歸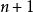 泊松回歸
泊松回歸 泊松回歸
泊松回歸此處, 是 維的向量,由 個獨立變數(自變數向量)一個常向量(元素取值全為1)構成,用一個 θ代表第一個表達式當中的 α和 β。
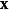 泊松回歸
泊松回歸因此,當已知泊松回歸模型當中的 θ和解釋變數 , 其滿足泊松分布的被解釋變數的期望值可以由下式來預測:
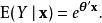 泊松回歸
泊松回歸Y是被解釋變數的觀測值,相應的解釋變數為 x,可由極大似然估計(Maximum Likelihood estimation)的方法來估計參數 θ。 極大似然估計不能通過解析表達式獲得解析解 ,是由其對數似然函式為凸函式的特性,可通過Newton–Raphson 或其他基於梯度下降的思想方法來進行參數估計。
極大似然估計
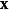 泊松回歸
泊松回歸如上所述,已知泊松回歸模型當中的 θ和解釋變數 , 其回歸表達式為:
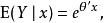 泊松回歸
泊松回歸泊松分布的機率密度函式為:
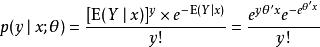 泊松回歸
泊松回歸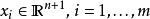 泊松回歸
泊松回歸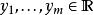 泊松回歸
泊松回歸現已知解釋變數的觀測值為由 m個向量組成 , 對應 m個被解釋變數的觀測值, . 若同時已知 θ, 則該組觀測值所對應的聯合機率可由下式表達:
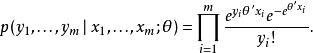 泊松回歸
泊松回歸極大似然方法估計 θ的核心思想是,去找到能使得基於當前觀測值的聯合機率儘可能達到最大的 θ。(可理解為:變數的取值當前觀測值,與取值為其他任何數值相比,是發生機率最高的事件)。 既然目標是尋找到最優的 θ,可以先將上式的等號左邊簡單表達為關於 θ的表達式:
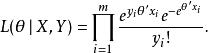 泊松回歸
泊松回歸注意等號右邊的表達式並未改寫,但通常難於付諸計算,因而採用其對數變化後的表達式( log-likelihood)即:
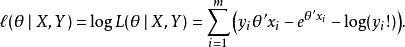 泊松回歸
泊松回歸由於 θ僅出現在似然函式的前兩項,因而在極大化似然函式的運算過程中,可以只考慮前兩項。可以刪去第三項 y!,待最佳化的似然函式可以簡潔表達為:
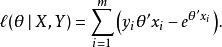 泊松回歸
泊松回歸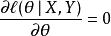 泊松回歸
泊松回歸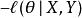 泊松回歸
泊松回歸為了找到極大值,需要求解方程:
可以通過對其似然函式取負值 (negative log-likelihood),是一個凸函式, 標準的凸最佳化方法可以考慮來求解θ的最優值。統一的方法是Newton-Raphson 與Iterative Weighted Least Square(IWLS)算法。 給θ一組初始值,IWLS 是通過多次疊代更新直到θ收斂。簡介
泊松回歸,並假設它期望值的對數可被未知參數的線性組合建模。泊松回歸模型有時(特別是當用作列聯表模型時)又被稱作對數-線性模型。
2014年世界盃,所有的數據分析專家都以數據為準,分析員最後都會將其整合成模型。通常情況下,建模人員會把問題從“哪一支隊伍會勝出”改為“X隊和Y隊比賽,X隊會進多少個球”,這裡使用到的是一種名為“雙變數泊松回歸分析法”(bivariate Poisson regression)。
“雙變數”指的是,在做出某個單一結果的預測時需要參考兩個相互影響的因素,比如一場比賽中的X隊和Y隊的表現。“回歸分析法”指將即有數據填充到模型中去。而“泊松分布”則是很有趣的分析方法。
試想像,你站在路旁,想要知道一分鐘會有多少汽車急馳而過。首先,你必須收集數據。利用秒表和計數器,第一分鐘,假設有15輛車駛過;第二分鐘,18輛;而下一分鐘只有4輛。持續記錄下去,你就可以得到一個模型,這便是“泊松分布”的原型。這項分析方法是由法國數學家西莫恩·德尼·泊松提出,用於估測人們做出錯誤判斷的幾率。
根據泊松分布,足球比賽的結果同樣具有分散性。一支足球隊進1或2個球的可能性最大,其次為不進或者進3個,而進4或5個球(或者更多)的幾率則大大下降。於是建模人員會根據這支隊伍之前的表現,通過泊松分布製圖,預測出它們之後得分的情況。
案例分析
觀眾們就開始預測結果並且在體育賽事上投下賭注;而近些年,一種與眾不同的數據分析法逐漸雄踞賽事預測市場。高盛,彭博以及納特·西弗尓的538(Five Thirty Eight)官網都利用數據,來對比賽的結果做出最為準確。高盛預測本土作戰的巴西有48.5%的幾率拿下冠軍;538給出的幾率是45%,而彭博認為巴西奪冠的幾率僅僅只有19.9%。