定義
 歐式環
歐式環一個整環叫做一個歐氏環 ,假如
 歐式環
歐式環 歐式環
歐式環(1) 有一個從的非零元所作成的集合到非負的整數集合的映射存在;
 歐式環
歐式環 歐式環
歐式環 歐式環
歐式環 歐式環
歐式環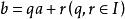 歐式環
歐式環(2)給定了的一個非零元,的任何元都可寫成的形式,
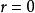 歐式環
歐式環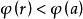 歐式環
歐式環這裡或者。
歐氏環就是能進行某種意義下的帶餘除法的環。在整數環和數域上的一元多項式環內都可進行帶餘除法
相關定理
 歐式環
歐式環1 任何歐氏環一定是一個主理想環,也一定是一個唯一分解環。
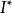 歐式環
歐式環 歐式環
歐式環證:設是的一個理想
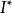 歐式環
歐式環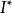 歐式環
歐式環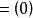 歐式環
歐式環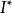 歐式環
歐式環(1)只包含零元,那么,是主理想;
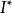 歐式環
歐式環 歐式環
歐式環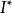 歐式環
歐式環 歐式環
歐式環(2)包含不為零的元,由歐氏環的定義,存在一個映射。在這個映射下,的每一個不為零的元
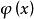 歐式環
歐式環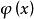 歐式環
歐式環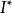 歐式環
歐式環都有一個象,且都是大於等於零的整數。所以必定存在最小的整數。因此我們可以找到
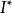 歐式環
歐式環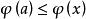 歐式環
歐式環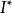 歐式環
歐式環的一個不為零的元,使得對於的任何不為零的元都有。在由歐氏環的定義,的
 歐式環
歐式環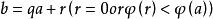 歐式環
歐式環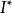 歐式環
歐式環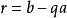 歐式環
歐式環每個元都可寫成。因為a,b都屬於,所以也
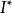 歐式環
歐式環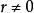 歐式環
歐式環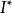 歐式環
歐式環 歐式環
歐式環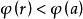 歐式環
歐式環 歐式環
歐式環屬於。若,則也有一個不等於零的元,滿足,與最小矛盾.
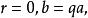 歐式環
歐式環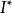 歐式環
歐式環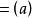 歐式環
歐式環所以,
2 一個域F上的 一元多項式環P[x]是歐氏環
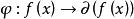 歐式環
歐式環證:利用多項式的次數,我們可規定一個符合條件的映射。
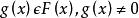 歐式環
歐式環假定
 歐式環
歐式環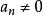 歐式環
歐式環 歐式環
歐式環 歐式環
歐式環那么的最高係數。但屬於域,域的每一個非零元都是一個單位,
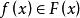 歐式環
歐式環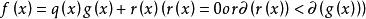 歐式環
歐式環所以,每一個,可表示為
例子
例1 整數環是歐氏環。
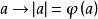 歐式環
歐式環證:存在映射:符合條件(1)
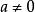 歐式環
歐式環 歐式環
歐式環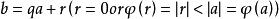 歐式環
歐式環給了整數,任意可表示為
例2 一個域是一個歐氏環。
證:因為域裡任意兩個非零元素是可以相除的 所以對於任意a,b且b≠0,存在q使得a=bq 所以令r=0即可,滿 足歐式環要求。
