基本介紹
自從1970年,Bellman與Zadeh提出模糊決策的概念之後,模糊最佳化一直是一個引人注目的研究領域。在這個領域中模糊線性規劃是一個發展較為成熟的領域,特別是用以求解模糊線性規劃的容差法(Tolerance Approach),不僅理論上比較完備,也在實際模糊決策中獲得了廣泛套用。
線性規劃已經廣泛地用於現代物流調運、資源最佳化配置、組合投資分析、區域經濟規劃等經濟領域。由於普通線性規劃的約束條件是固定的,在經濟發展過程中必然會出現一些波動,因此實際問題需要約束條件具有一定的彈性,目標函式可能不是單一的,可以藉助於模糊集合的方法來處理。引入隸屬函式概念,將線性規劃的約束條件與目標函式模糊化,進而導出一種新的線性規劃問題,它的最優解稱為原問題的模糊最優解。
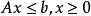 模糊線性規劃
模糊線性規劃 模糊線性規劃
模糊線性規劃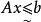 模糊線性規劃
模糊線性規劃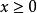 模糊線性規劃
模糊線性規劃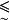 模糊線性規劃
模糊線性規劃對於通常的線性規劃問題,即在約束條件下,求目標函式的極值min Z,考慮約束條件的軟化,,這裡“”表示對“≤”的一种放寬,並確定它的隸屬函式為
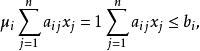 模糊線性規劃
模糊線性規劃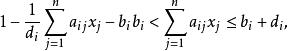 模糊線性規劃
模糊線性規劃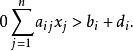 模糊線性規劃
模糊線性規劃這即是 模糊線性規劃問題 。
模糊線性規劃的模型
模糊約束線性規劃的一般形式如下 :
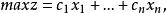 模糊線性規劃
模糊線性規劃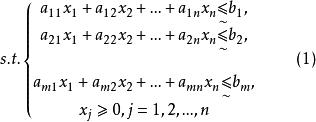 模糊線性規劃
模糊線性規劃模糊線性規劃的模型可簡記為:
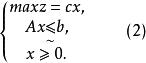 模糊線性規劃
模糊線性規劃模糊線性規劃的求解
下面我們來討論式(2)的求解問題 。
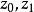 模糊線性規劃
模糊線性規劃設分別是普通線性規劃,即
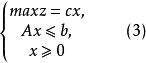 模糊線性規劃
模糊線性規劃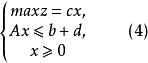 模糊線性規劃
模糊線性規劃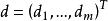 模糊線性規劃
模糊線性規劃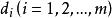 模糊線性規劃
模糊線性規劃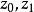 模糊線性規劃
模糊線性規劃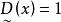 模糊線性規劃
模糊線性規劃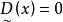 模糊線性規劃
模糊線性規劃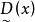 模糊線性規劃
模糊線性規劃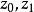 模糊線性規劃
模糊線性規劃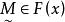 模糊線性規劃
模糊線性規劃的最優值,其中稱為式(2)的 伸縮指標向量。為第i個伸縮指標。對應兩種極端情況,一種是完全接受約束),另一種是完全不接受約束(),它們都不是我們所希望的。我們的目的是適當減低隸屬度,使得最優值有所提高且介於之間,為此構造模糊目標集,其隸屬度為
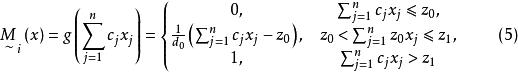 模糊線性規劃
模糊線性規劃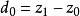 模糊線性規劃
模糊線性規劃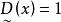 模糊線性規劃
模糊線性規劃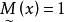 模糊線性規劃
模糊線性規劃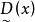 模糊線性規劃
模糊線性規劃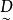 模糊線性規劃
模糊線性規劃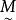 模糊線性規劃
模糊線性規劃 模糊線性規劃
模糊線性規劃 模糊線性規劃
模糊線性規劃其中,。易見,當時,,這表明欲使目標值大於z必須降低。為了兼顧模糊約束集與模糊目標集,可採用模糊判決,然後選擇,使
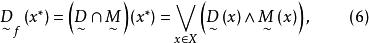 模糊線性規劃
模糊線性規劃注意到
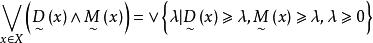 模糊線性規劃
模糊線性規劃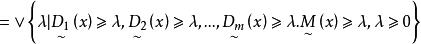 模糊線性規劃
模糊線性規劃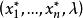 模糊線性規劃
模糊線性規劃於是問題歸結為求普通線性規劃問題,若求出普通線性規劃問題的最優解為,則
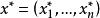 模糊線性規劃
模糊線性規劃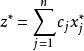 模糊線性規劃
模糊線性規劃為式(3)的最優解,得式(3)的最優解。