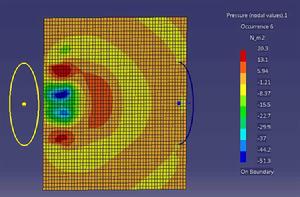
簡介
有限元計算的任務是基於有限元模型完成有關的數值計算,並輸出需要的計算結果。它的主要工作包括單元和總體矩陣的形成、邊界條件的處理和特性方程的求解,由於計算的運算量非常大,所以這部分工作由計算機完成。除計算前需要對計算方法、計算內容、計算參數和工況條件等進行必要的設定和選擇外,一般不需要人的干預。
有限元計算步驟
離散化
首先是將需要分析的模型離散化,離散化是指將連續的彈性體劃分成有限個單元組成的離散體,並把作用力按等效原則移置到各節點上 。
單元分析
接著進行單元分析,了解一個單元里節點力和節點位移的關係。單元分析的任務是通過節點位移來表示單元內部任一點的位移,從而建立起節點力和節點位移之間的轉換關係 。
單元綜合
最後是單元綜合,即利用節點平衡方程式,在已知節點力的情況下,聯繫邊界條件,求出節點位移,然後求得各單元應力或節點應力。
因為節點數可以從幾個到幾百個、上千個,所以有限元計算中必需套用計算機 。
有限元分析系統計算模組
計算模組由一系列計算程式組成,計算程式又稱求解器(solver)。每個求解器完成特定類型的計算。因此,求解器越多,系統功能越豐富。在有限元模型提交計算以前,計算模組還提供計算定義功能,用於選擇算法、參數、精度、輸出結果、結果保留形式等。
目前常見的計算類型包括如下:
①線性靜力分析
②動態分析
③非線性分析(材料非線性,幾何非線性,接觸非線性)
④熱分析
⑤流場分析
⑥電磁場分析
⑦曲屈分析