定義
設
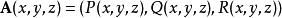 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場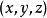 旋度場
旋度場為空間區域 上的向量函式。對 上每一點 ,定義向量函式
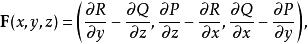 旋度場
旋度場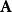 旋度場
旋度場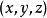 旋度場
旋度場稱它為向量函式 在 處的旋度,記作
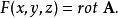 旋度場
旋度場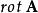 旋度場
旋度場註記 rot是rotation(旋度)一詞的縮寫,有的書也用curl表示旋度,為便於記憶, 可形式地寫成
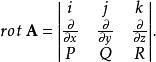 旋度場
旋度場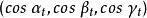 旋度場
旋度場 旋度場
旋度場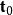 旋度場
旋度場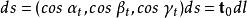 旋度場
旋度場設 是曲線 的正向上的單位切線向量 的方向餘弦,向量 稱為 弧長元素向量。於是斯托克斯公式可寫成如下向量形式:
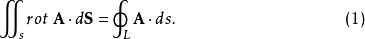 旋度場
旋度場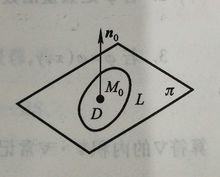 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場為了說明旋度與坐標系的選取無關,我們在場 中任意選取一點 ,
 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場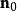 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場通過 作平面 垂直於曲面 的法向量 (如右圖),且在 上圍繞 作任一封閉曲線 ,記 所圍區域為 ,則由(1)式有
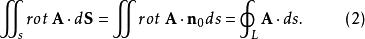 旋度場
旋度場對左端曲面積分套用中值定理可得
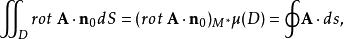 旋度場
旋度場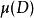 旋度場
旋度場 旋度場
旋度場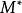 旋度場
旋度場 旋度場
旋度場其中, 為區域 的面積, 為 中的某一點。因此
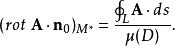 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場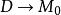 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場現讓 收縮到點 (記作 )時,於是 趨於 ,因此有
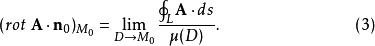 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場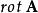 旋度場
旋度場(3)式左邊為 在法線方向上的投影,因此它也確定了 的本身,所以(3)也可以作為旋度的另一種定義形式。由於(3)式右邊極限與坐標系的選取無關,故 也與坐標系的選取無關。
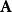 旋度場
旋度場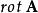 旋度場
旋度場由向量函式 的旋度 所定義的向量場,稱為 旋度場 。
在流量問題中,我們稱
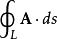 旋度場
旋度場 旋度場
旋度場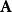 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場為沿閉曲線 的環流量,它表示流速為 的不可壓縮流體在單位時間內沿曲線 的流體總量,反映了流體沿 時的旋轉強弱程度。當 時,沿任意封閉曲線的環流量為零,即流體流動時不成旋渦,這時稱向量場 為 無旋場 。
公式(2)表明向量場在曲面邊界線上的切線投影對弧長的曲線積分等於向量場的旋度的法線投影在曲面上對面積的曲面積分。它的物理意義可以說成是:流體的速度場的旋度的法線投影在曲面上對面積的曲面積分等於流體的曲面邊界上的環流量。
 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場 旋度場
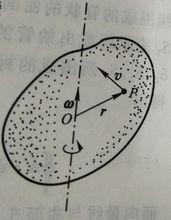
旋度場為了更好地認識旋度的物理意義以及這一名稱的來源,我們討論剛體繞定軸旋轉的問題。設一剛體以角速度 繞某軸旋轉,則角速度向量 方向沿著旋轉軸,其指向與旋轉方向的關係符合右手法則,即右手拇指指向角速度 的方向,其他四指指向旋轉方向。若取定旋轉軸上一點 作為原點(如右圖),剛體上任意一點 的線速度可表示為
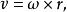 旋度場
旋度場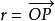 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場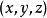 旋度場
旋度場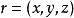 旋度場
旋度場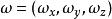 旋度場
旋度場其中 是 的徑向量。設 的坐標為 ,便有 ,又設 。於是
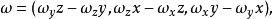 旋度場
旋度場所以
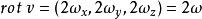 旋度場
旋度場或
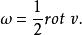 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場這等式表明線速度向量 的旋度除去一個常數因子 外,就是旋度的角速度向量 。可見 的旋度與 稱正比,這也說明了旋度這個名稱的來源。
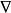 旋度場
旋度場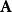 旋度場
旋度場套用算符 表示 的旋度是
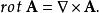 旋度場
旋度場旋度的性質
不難證明旋度具有下列一些性質 :
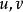 旋度場
旋度場1、 若是向量函式,則
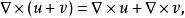 旋度場
旋度場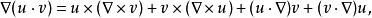 旋度場
旋度場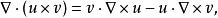 旋度場
旋度場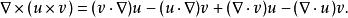 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場2、 若是數量函式,是向量函式,則
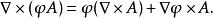 旋度場
旋度場 旋度場
旋度場 旋度場
旋度場3、若是數量函式,是向量函式,則
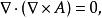 旋度場
旋度場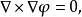 旋度場
旋度場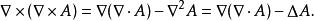 旋度場
旋度場