概念
施泰納最小樹問題(Steiner shortest treeproblem)是一類組合最佳化問題。在平面上有n個點，問在平面上需增添多少個點，使可以連這n個點和增加的點而得到長度最短的樹。這就是施泰納最小樹問題。除了只有一、兩個點的不足道的情形外，最簡單的情形為三、四個點。若三個點不在一條線上，則要增添一個點P。如下左圖中實線所示，給出了施泰納最小樹。若四個點中沒有三個點在一條直線上，則要增添兩個點p，q而得到施泰納最小樹，如下右圖實線所示。一般情形也可以用物理上的表面張力原理做實驗而得到。但時至今日在數學上仍沒有得到解答。
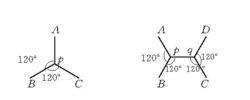施泰納最小樹問題組合最佳化問題
一類離散狀態下的極值問題。已知有限元素集E，對於E的每個元素e關聯著一個目標係數c(e)，可視為價格、價值、權值、距離等。E的某類特定子集組成集族F，稱為問題的可行解集。問題是在F中尋求某個元素F，使在F上實現目標值的極大或極小。它可表示為：
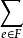施泰納最小樹問題min或(max)c(e)|F∈F.
簡記為三元組(E，F，c)。因為E為有限集，組合最佳化的最優解總是存在的。但是，對於許多組合最佳化的具體問題來說，F中元素的數目非常巨大以至於人們不可以採用窮舉比較的辦法來求出最優解。因此，組合最佳化的主要任務是：或者設計出特有的算法，以有效地求出該問題的最優解；或者是證明根本就不存在比窮舉更好的算法。組合最佳化早期研究的問題來自運籌學、工業管理、邏輯學、工程學、計算機科學以及軍事套用等領域。之後它又廣泛地聯繫著其他眾多領域，並獲得成功的套用，例如生物學、化學、經濟學、地質學、語言學、物理學、社會學等。它表現出兩個突出的特點：一個是它的廣泛套用性；另一個是現實世界裡的組合最佳化問題大部分都很難求解。由於這兩個特點的刺激，使得組合最佳化的研究和成果、發展與變化非常迅速。典型的組合最佳化問題有獨立系統問題、擬陣問題、支撐樹問題、匹配問題、二擬陣交問題、二部圖匹配或指派問題、b匹配問題、最短路問題、網路流問題、中國郵路問題、旅行售貨員問題、一般路徑問題、時間表問題、選址問題、集合覆蓋、集合劃分、集合裝箱問題、節點覆蓋、節點劃分、節點裝箱問題、染色問題、背包問題、圖的嵌入問題、布局問題等。
施泰納
瑞士—德國數學家。生於瑞士伯爾尼州的烏岑斯多夫，卒於伯爾尼。出身於貧苦農民家庭，14歲前在家放牧，沒有受過教育。但他有很強的計算能力，十分渴望讀書。18歲時離家出走，幸遇著名教育家裴斯泰洛齊 (J.H.Pestalo-zzi)，被吸收到他的學校學習。由於裴斯泰洛齊教學有方，施泰納很快便對數學產生濃厚興趣。他不久便兼任該校數學教師，受到學生歡迎。後來，學校因經濟困難而停辦。施泰納於1818年到德國海德堡靠當家庭教師為生自修幾何學。1822年入柏林大學學習。1832年獲柯尼斯堡大學榮譽博士學位。1834年任柏林大學特任教授並進入柏林科學院。施泰納是近代射影幾何學的奠基人。他的主要著作《幾何圖形相互依賴性的系統發展》(1832)深刻地討論了對偶原理。他建立射影幾何的嚴密系統，推廣卡諾完全四邊形的工作到空間多邊形上去，完成了點列、線束、二次曲線及曲面的理論，討論圓錐曲線和“帕斯卡六角形”的性質。由於他在幾何方面的重要貢獻，被譽為自阿波羅尼奧斯以來最偉大的幾何學家。施泰納推崇純粹綜合幾何方法，強調幾何直觀，反對解析方法，但思想走向極端。他不承認有正負號的和虛的幾何元素，指斥它們是“幾何學中的鬼域”，他甚至厭惡代數的或分析的推導。他是當時幾何學中“綜合”與“解析”之爭中“綜合”派的代表人物。這場論爭反映了當時幾何學發展的水平及其局限性，同時也促進了幾何學的進一步發展。
