復微分p形式

叢ΛCT*(M)的截面就稱為M上的復微分p形式（complex differential p-form），p≥0。

簡介

復微分p形式是一種截面。

叢Λ T*(M)的截面就稱為M上的復微分p形式，p≥0。

性質

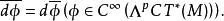復微分p形式

外微分復化後給出復微分形式上的運算元，仍記為d，運算元d的性質與實流形的外微分運算的性質相同，此外它是實的，即

截面

當需要考察對末態的運動參量加某種限制時的截面變化率，這就導致微分截面的概念。例如在彈性散射中，在空間某特定方向單位立體角的散射截面就是一種描寫角分布的微分截面。

當需要考察對末態進行不連續變化的分類截面時，就導致部分截面的概念。例如在研究散射問題時，當把散射過程按碰撞角動量來分解，則截面就可表示成各種角動量對截面貢獻之和，這種給定角動量的截面就是一種部分截面。