基本介紹
取整函式
 小數部分函式
小數部分函式 小數部分函式
小數部分函式 小數部分函式
小數部分函式設,定義函式表示不超過的最大整數,稱之為 取整函式,取整函式也稱 高斯函式。例如:
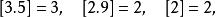 小數部分函式
小數部分函式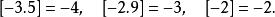 小數部分函式
小數部分函式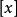 小數部分函式
小數部分函式 小數部分函式
小數部分函式 小數部分函式
小數部分函式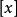 小數部分函式
小數部分函式 小數部分函式
小數部分函式在數軸(箭頭向右)上,是在點或其左側的第一個整數點,當是整數時就是,圖像如圖1 。
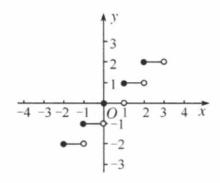 圖1 取整函式
圖1 取整函式小數部分函式
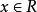 小數部分函式
小數部分函式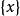 小數部分函式
小數部分函式設,定義函式為
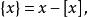 小數部分函式
小數部分函式 小數部分函式
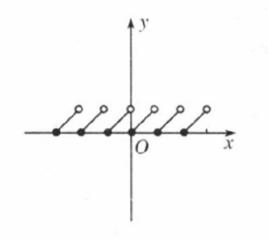
小數部分函式稱之為 小數部分函式,它表示的是的小數部分。圖像如圖2 。
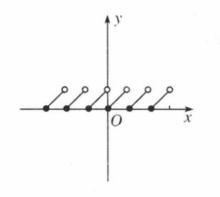 圖2
圖2 小數部分函式
小數部分函式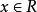 小數部分函式
小數部分函式任意實數都能寫成整數與非負純小數之和,即任意,
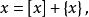 小數部分函式
小數部分函式而且
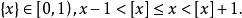 小數部分函式
小數部分函式取整函式和 小數部分函式是最簡單的數論函式。
相關性質
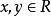 小數部分函式
小數部分函式 小數部分函式
小數部分函式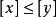 小數部分函式
小數部分函式性質1,若,則。
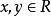 小數部分函式
小數部分函式性質2,有
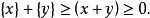 小數部分函式
小數部分函式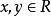 小數部分函式
小數部分函式性質3,有
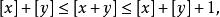 小數部分函式
小數部分函式並且兩個等號不可能同時成立。
性質4
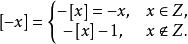 小數部分函式
小數部分函式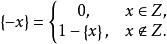 小數部分函式
小數部分函式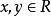 小數部分函式
小數部分函式性質5,有
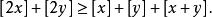 小數部分函式
小數部分函式性質6若n為整數,則
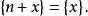 小數部分函式
小數部分函式性質7
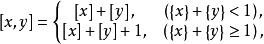 小數部分函式
小數部分函式性質8n為自然數,則
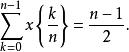 小數部分函式
小數部分函式對於取整函式,還有如下定理。
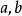 小數部分函式
小數部分函式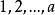 小數部分函式
小數部分函式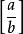 小數部分函式
小數部分函式定理1設為兩個正整數,則在中能被b整除的數的個數k為。
 小數部分函式
小數部分函式定理2 設b是一個正整數,則任意整數必能表示為
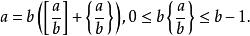 小數部分函式
小數部分函式 小數部分函式
小數部分函式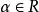 小數部分函式
小數部分函式定理3 設是任意正整數,若,則
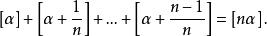 小數部分函式
小數部分函式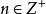 小數部分函式
小數部分函式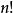 小數部分函式
小數部分函式定理4 設,在的標準分解式中,素數p的指(次)數為
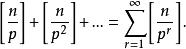 小數部分函式
小數部分函式初等函式與非初等函式
初等函式
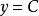 小數部分函式
小數部分函式(1)基本初等函式,共有6類,它們是:①常數函式;②冪函式;③指數函式;④對數函式;⑤三角函式(正弦函式,餘弦函式,正切函式,餘切函式,正割函式,餘割函式);⑥反三角函式(反正弦函式,反餘弦函式,反正切函式,反餘切函式)。
(2)初等函式:凡由基本初等函式經過有限次的四則運算和有限次的複合運算得到的函式都稱為初等函式。
常見的非初等函式
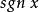 小數部分函式
小數部分函式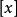 小數部分函式
小數部分函式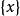 小數部分函式
小數部分函式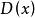 小數部分函式
小數部分函式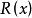 小數部分函式
小數部分函式常見的非初等函式如下:符號函式,整數部分函式, 小數部分函式,狄利克萊(Dirichlet)函式,黎曼(Riemann)函式。一般而言,分段函式是非初等函式 。