簡介
液體的理論遠不如氣體理論研究得那樣充分。雖然體積為三次冪的狀態方程，如范德華方程和Redlich-Kwong方程等也能定性地描述液體的P、V、T行為，但一般來說，不能定量地計算遠離臨界態和具有較高的對比密度的液體性質。Benedict-Webb-Rubin方程雖可用於液體，但計算複雜，對於每一種液體都要計算出八個常數後方能套用。為此，必須研究適合於工程計算所需的方程。
雷克特液體狀態方程
通用方程式
容積性質
容積性質Rackett提出了飽和溶液的摩爾體積的通用方程式為： 其中，是飽和溶液的摩爾體積。
優點
只需要臨界參數，就可計算在不同溫度下的飽和溶液的摩爾體積，Rackett曾對十六種不同性質的液體進行計算，其中包括高極性物質，如氨、丙酮和氰化氫等，最大誤差為7%左右，不少物質的計算誤差在2%以內。但
缺點
本方程對醇類、腈類和羧酸類都不適用，因為這些都是締合液體如羧酸和腈類在液相中可能成為雙聚物，醇類分子也會相互結合而形成大的基團。該方程式也不適合於量子效應很強的氦和氫。
改良的Rackett方程
Uunn-Yamada等曾對Rackett方程作了某些修正，成為改良的Rackett方程，其形式為：
容積性質
容積性質
容積性質其中是對比溫度下的液體摩爾體積。這個簡單的方程精度相當高，對許多非極性的飽和液體來說，誤差在1%以內。
典例
容積性質估計150℃時乙硫醇液體的摩爾體積。已知實驗值為。
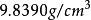容積性質
容積性質註：查得乙硫醇的臨界參數為，20℃時的飽和液體密度為。
按Rackett方程計算
（1）摩爾體積為：
容積性質
容積性質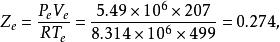
容積性質（2）計算誤差為：
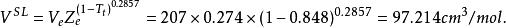容積性質按改良的Rackett方程計算
（1）摩爾體積為：
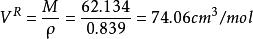容積性質
容積性質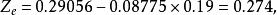
容積性質
容積性質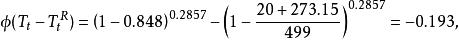（2）計算誤差為：
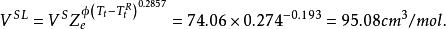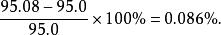容積性質