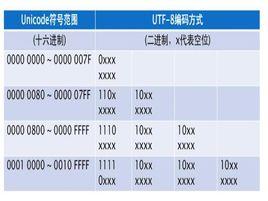
編碼簡介
在顯示器上看見的文字、圖片等信息在電腦裡面其實並不是我們看見的樣子,即使你知道所有信息都存儲在硬碟里,把它拆開也看不見裡面有任何東西,只有些碟片。假設,你用顯微鏡把碟片放大,會看見碟片表面凹凸不平,凸起的地方被磁化,凹的地方是沒有被磁化;凸起的地方代表數字1,凹的地方代表數字0。硬碟只能用0和1來表示所有文字、圖片等信息。那么字母”A”在硬碟上是如何存儲的呢?可能小張計算機存儲字母”A”是1100001,而小王存儲字母”A”是11000010,這樣雙方交換信息時就會誤解。比如小張把1100001傳送給小王,小王並不認為1100001是字母”A”,可能認為這是字母”X”,於是小王在用記事本訪問存儲在硬碟上的1100001時,在螢幕上顯示的就是字母”X”。也就是說,小張和小王使用了不同的編碼表。小張用的編碼表是ASCII,ASCII編碼表把26個字母都一一的對應到2進制1和0上;小王用的編碼表可能是EBCDIC,只不過EBCDIC編碼與ASCII編碼ψ的字母和01的對應關係不同。一般地說,開放的作業系統(LINUX、WINDOWS等)採用ASCII編碼,而大型主機系統(MVS、OS/390等)採用EBCDIC編碼。在傳送數據給對方前,需要事先告知對方自己所使用的編碼,或者通過轉碼,使不同編碼方案的兩個系統可溝通自如。
ASCII碼使用7位2進制數表示一個字元,7位2進制數可以表示出2的7次方個字元,共128個字元。EBCDIC碼使用8位,可以表示出2的8次方個字元,256個字元。
無論是ASCII碼還是EBCDIC碼,都無法對擁有幾萬個的漢字進行編碼。因為上面已經提過,7位2進制數最多對應上128個字元,8位最多對應上256個字元。
英文字母編碼方案
直觀編碼
由A到Z依次可編碼,如圖所示。
 直觀編碼A~W
直觀編碼A~W 直觀編碼XYZ
直觀編碼XYZ陣列編碼
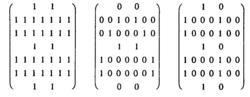 陣列編碼
陣列編碼由A到Z依次可編碼,如圖所示。
二進編碼
ψ(Ω)=111111111111111111111111111111111
ψ(A)=0000010010001001101010000101000001
ψ(B)=0100100010010001010010001001000101
ψ(C)=1010100001010000000010000001000111
ψ(D)=0100100010010000100010001001000101
ψ(E)=1010100000010000101010000001000011
ψ(F)=1010100000010000101010000001000000
ψ(G)=101000001010000001010000101000111
ψ(H)=0000100001010001101010000101000100
ψ(I)=0000000100000010000000010000100000
ψ(J)=0000000100000010000000010000001001
ψ(K)=000100100010000000101000010010000
ψ(L)=0000100000010000000010000001000001
ψ(M)=0001010101101010010010000101000001
ψ(N)=0001010010100100010010010101000101
ψ(O)=0100100100010010000010010001001011
ψ(P)=0100100100010010010010000001000000
ψ(Q)=0000010010001000100001010100101010
ψ(R)=0100100010010001010010001001000010
ψ(S)=0100100100010000001000010001001001
ψ(T)=0101000100000010000000010000001000
ψ(U)=0000100001010000010010000101000111
ψ(V)=0000100010100000010001000100100100
ψ(W)=0000100001010000010101011010100101
ψ(X)=0000010001001001000001001000100010
ψ(Y)=0000010001001001000000010000001000
ψ(z)=01010000010000010000001000001000
絕對碼重
 字母編碼
字母編碼由A到Z依次可編碼,如圖所示。
相對碼重
 字母編碼
字母編碼由A到Z依次可編碼,如圖所示。
中文字母編碼
漢字編碼史
漢字編碼回溯到我國東漢時期,許慎首創部首編排法,將9353個漢字劃分為540部,編出我國第一部系統分析漢字字形的字典《說文解字》。由於這種編排法揭示了漢字複雜的內部結構,因而流傳至今。現在出版的有些字典只不過將部首略作刪改,如《新華字典》改為189部,《現代漢語詞典》改為188部。然而,部首編排法查字速度太慢,更談不上見字識碼。原商務印書館長王雲五創四角號碼檢字法,第一次解決了“見字識碼”的問題。這種編碼法現在仍是權威性的編碼法之一,除了《四角號碼新詞典》採用以外,《現代漢語詞典》在書前,新版《辭源》在書後均附有四角號碼檢字表。不過,這種編碼的重碼率太高,不能滿足電子計算機的要求。
要知道,造成重碼的原因是多方面的。就以“王”、“豆”兩字的編碼為例,它們的編碼都是1010,造成同碼的原因為:(1)四角號碼法只考慮了漢字四角的特點,而忽略了漢字的內部結構。然而,“王”與“豆”的根本區別正是在內部。(2)對這兩字名義上是取四角,但所取的角中只有左上、左下兩角生效。
樹形編碼
從以上對漢字編碼史的回顧,我們得出如下結論:只有抓住漢字字形複雜的內部結構這一根本點,才可能得出先進的編碼方案。“漢字樹形結構中文字母編碼法”(簡稱“樹”法)正是在總結我國編碼史的基礎上提出來的。它以漢字結構文法及其語法樹為理論基礎,直接將三十六對中文字母(從數萬漢字中提煉出,每對中文字母只對應一個數字或一個英文字母)作為漢字的編碼,並共用現成的英文鍵盤。
象物質由分子組成一樣,漢字由幾個小塊複合而成。這些構字小塊簡稱塊。塊的形狀多樣,有矩形、三角形、凹多邊形諸種。塊內筆劃之間相互關係錯綜複雜。那些筆劃之間縱橫相交或相連的塊,如“豐”、“王”、“藝”……都是交連塊。筆劃分離的塊如“甲”、“三”、“立,.··…等都是離散塊。塊內有塊的那些塊如“國”,“田”……是相套塊。塊與塊彼此相嵌的塊,如“臾”是相嵌塊。上述這些塊合稱分塊。
對數萬漢字進行分解的結果,從中提煉出三十六對字元,作為中文字母。中文字母成對出現,每對字母對應一個數字或一個英文字母。換言之,每對中文字母對應於同一個ASClI碼。中文字母分成兩類,甲類為三十六個常用符號,乙類為三十六個大容量的偏旁部首,且為漢字,如“木,之”等。對《新華字典》71年修訂重排本“部容量”作了一個統計。該字典收字8500左右,將漢字分為189部,在中文字母中所出現的偏旁部首總容量為7955字,占整個字典總容量的93.59%。這說明中文字母具有極強的構字能力。甲類符號又分為四區。
如果一漢字不是分塊,那么對它進行樹形結構的一級分解。設LEAE(CW)={B,B,…B},這裡N=2,3,4,5
1.1若N=2,對B、B分別進行二級分解,限分兩塊。轉3.
1.2若N>3,轉3。
2.如果一漢字是一分塊,那么對它進行二級分解。
3.取每塊為首的最大字母為其編碼。
“樹”法方法簡明,不用記憶,識碼高速。不管是哪一個國家的人,只要他能正確書寫漢字,就能按書寫分塊的先後次序,對漢字進行樹形結構的一級分解並進行編碼,其速度不低於書寫一個英文字的速度。
樹”法平均碼長短且重碼率低。“樹”法不局限於對漢字幾個“角”的了解,它對漢字進行了層層剖析,將漢字分解為分塊,又將分塊繼續分解為原子塊,深刻地揭示了漢字複雜的內部結構。因而,收到了平均碼長短且重碼率低的效果。以一九八二年五月出版的《快速集中識字手冊》的六千多漢字為例,重碼率僅0.3%,平均碼長2.5。
“樹”法對高頻漢字以及大容量部首都進行了巧妙安排。而且高頻漢字的編碼直接由“樹”法規則決定,且編碼長度短,不必另設簡碼錶。前20個高頻漢字的平均碼長僅1.75。