簡介
物理學中, 威克轉動(Wick rotation)是一個找尋解的方法,將閔可夫斯基空間中的問題轉到歐幾里得空間中,於其中求解,再逆轉回閔可夫斯基空間中。其所根據的是解析延拓(analytic continuation)。
其動機來自於對表達閔可夫斯基空間的度規所做的觀察,閔可夫斯基度規如下:
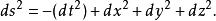 威克轉動
威克轉動而四維歐幾里得度規為:
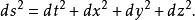 威克轉動
威克轉動若允許座標{\displaystyle t}可以具有複數值,則兩者並無不同。當{\displaystyle t}被限制在虛數軸上時,閔可夫斯基度規變成了歐幾里得度規,反之亦然。若以閔可夫斯基空間中座標{\displaystyle x,y,z,t}表示一問題,然後將{\displaystyle w=it}帶入,有時候即可產生在實數歐幾里得座標{\displaystyle x,y,z,w}所表示的問題,而這樣比較容易得到解。這樣的解可以在之後,透過反向的帶入,產生原本問題的解。
威克轉動以驚人地方式連結了量子力學與統計力學。舉例來說,薛丁格方程式(Schrödinger equation)與熱方程式(heat equation)可透過威克轉動而相關連。然而,仍有些許差異,例如:統計力學中的n點函式滿足正性(positivity),而威克轉動下的量子場論(quantum field theory, QFT)則滿足反射正性(reflection positivity)。Template:Elucidate
威克轉動是以義大利科學家吉安·卡羅·威克為名。它被稱作“轉動”(rotation)是因為當我們將複數表示成平面時,將一複數乘上{\displaystyle i}等於將代表此複數的向量旋轉了{\displaystyle \pi /2}的角度。
當史蒂芬·霍金(Stephen Hawking)在他的知名著作《時間簡史》( A Brief History of Time)中寫下關於“虛數時間”的東西時,他所用到的就是威克轉動。
威克轉動亦將一個處於一有限的溫度倒數(inverse temperature)β之量子場論聯繫到一在“管” R×S上的統計力學模型,其中虛數時間座標τ具有周期性,周期為β。
不過要注意到,不能將威克轉動視為在複數向量空間的轉動;複數向量空間具有平常的範數以及由內積又導出的度規,在此之中威克轉動會抵銷調而沒有任何的效應。
解析延拓
解析延拓是數學上將解析函式從較小定義域拓展到更大定義域的方法。透過此方法,一些原先發散的級數在新的定義域可具有迥異而有限的值。其中最知名的例子為Γ函式與黎曼ζ函式。
若 f為一解析函式,定義於複平面 C中之一開子集 U,而 V是 C中一更大且包含 U之開子集。 F為定義於 V之解析函式,並使
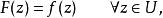 威克轉動
威克轉動則 F稱為 f之解析延拓。換過來說,將 F函式限制在 U則得到原先的 f函式。
解析延拓具有唯一性:
若 V為兩解析函式 F及 F的連通定義域,並使 V包含 U;若在 U中所有的 z使得 F( z) = F( z) = f( z),則在 V中所有點 F= F。
此乃因 F− F亦為一解析函式,其值於 f的開放連通定義域 U上為0,必導致整個定義域上的值皆為0。此為全純函式之惟一性定理的直接結果。
相關條目
•史溫格函式(Schwinger function)
•虛時間
