定義
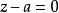多重極點
多重極點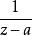
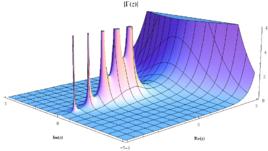
多重極點 多重極點亞純函式的 極點是一種特殊的奇點，它的表現如同 時 的奇點。這就是說，如果當 z趨於 a時，函式 趨於無窮大，那么 在 z= a處便具有 極點。
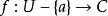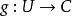多重極點
多重極點假設 U是複平面 C的開子集， a是 U的一個元素， 是一個在定義域內全純的函式。如果存在一個全純函式 和一個非負整數 n，使得對於所有 U− { a}內的 z，都有
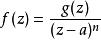多重極點那么 a便稱為f的極點。滿足以上條件的最小整數 n稱為極點的階。一階的極點又稱為簡單極點，零階的極點又稱為可去奇點。當n的值大於1時，a便是f的 多重極點。
從以上的定義，我們可以推出一些特徵：
如果 a是 n階極點，則在以上的表達式中必有 g( a) ≠ 0。因此，我們有
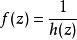多重極點其中 h是在 a的開鄰域內全純的函式，在 a處具有 n階零點。
另外，由於 g是全純函式， f可以表示為：
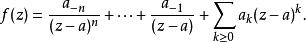多重極點這是一個洛朗級數，它的主部分是有限的。全純函式∑ a( z - a)稱為 f的正則部分。因此，點 a是 f的 n階極點，若且唯若 f在 a處的羅朗級數中所有低於− n的次數都為零，而− n次項不為零。
相關性質
•如果函式f的一階導數在a處具有簡單極點，則a是f的一個分支點，但反過來不成立。
•一個既不是極點又不是分支點的非可去奇點稱為本性奇點。
•除了一些孤立奇點外全純的函式，且所有的奇點均為極點，則該函式稱為亞純函式。
洛朗級數
多重極點在數學中，複變函數的洛朗級數，是冪級數的一種，它不僅包含了正數次數的項，也包含了負數次數的項。有時無法把函式表示為泰勒級數，但可以表示為洛朗級數。洛朗級數是由皮埃爾·阿方斯·洛朗在1843年首次發表並以他命名的。
多重極點函式f(z)關於點c的洛朗級數由下式給出：
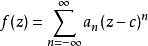多重極點
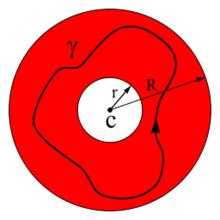
多重極點其中是常數，由以下的曲線積分定義，它是柯西積分公式的推廣：
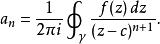多重極點
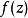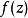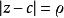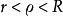多重極點 多重極點
多重極點 多重極點
多重極點
多重極點 多重極點
多重極點 多重極點積分路徑γ是位於圓環A內的一條逆時針方向的可求長曲線，把c包圍起來，在這個圓環內是全純的（解析的）。的洛朗級數展開式在這個圓環內的任何地方都是正確的。在右邊的圖中，該環用紅色顯示，其內有一合適的積分路徑 。如果我們讓是一個圓 ，其中，這就相當於要計算的限制到上的復傅立葉係數。這些積分不隨輪廓的變形而改變是斯托克斯定理的直接結果。
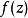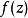多重極點 多重極點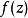 多重極點 多重極點在實踐中，上述的積分公式可能不是計算給定的函式係數最實用的方法；相反，人們常常通過拼湊已知的泰勒展開式來求出洛朗級數。因為函式的洛朗展開式只要存在就是唯一的 ，實際上在圓環中任何與相等的，以上述形式表示的給定函式的表達式一定就是的洛朗展開式。
