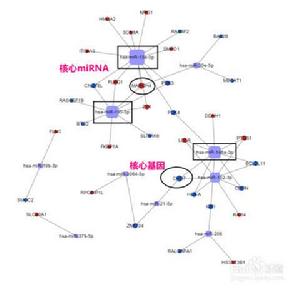
建立布爾網路模型的一個主要目標就是設計各種干預策略來影響網路長期行為,從而用於疾病診斷和藥物研發。干預可以改變網路使其往期望的方向發展,但同時對網路進行隨機的干預也會使遺傳網路發展為不期望的結果 。
在系統演化過程中有一個很重要的概念,那就是吸引子。通常情況下,吸引子(attractor)指的是,從任一初始狀態開始,最終都可以到達某些狀態並始終停留在原地的狀態。在布爾網路中,通常用吸引子來表示動態系統的一個固定點,即一種長期行為,任何其他的狀態經過演化都會到達這些吸引子。根據吸引子中狀態的個數,可以分為單吸引子(singleton attractor)和吸引環(cyclic attractor)。同時,吸引子總是有周期的,吸引子的周期(cycle length)可以定義為:如果以一個吸引子狀態作為起點開始演化,直到最終到達的狀態仍是它本身,那么這期間所經過的狀態次數即是吸引子的周期。通常情況下,單吸引子的周期就是1,而吸引環的周期就不確定了,它是由環內所包含的吸引子狀態的個數決定的(大於1) 。
Kauffman曾提出一個看法,他覺得BN中的吸引子能夠在一定程度上代表出細胞的類型。並且目標基因的表達值決定了該類型是否是期望的。因此,網路空間可以被分成兩部分:期望狀態集D和不期望狀態集U。我們的目的是通過對網路進行一定的干預,使網路能夠逆向回到原來的狀態或轉移到另外一個期望的狀態,減少U部分的穩態機率,並最終改善網路長期動態行為。因此為了達到這一目標,我們現在面臨的難題就是如何對網路進行干預。
干預方法分為三種:基因干預,結構干預和外部干預。基因干預是瞬時干預,它只能使基因的當前狀態發生改變,而無法改變網路的長期動態行為;結構干預和外部干預屬於持久干預,它們能夠改變網路的長期動態行。
近年來,採用調控的方法使基因調控網路的狀態從一個吸引子進入另一吸引 子成為研究的熱點。
定義
採用調控的方法使基因調控網路的狀態從一個吸引子進入另一吸引 子稱為吸引子調控。
在基因調控網路模型中,通過基因單點(或者多點)調控實現吸引子狀態的切換分別稱為單點吸引子調控和多點吸引子調控。
性質
一個由n個節點和1個外界輸入u(t)所組成的布爾網路,可以描述為以下的形式:
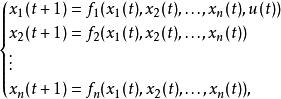 吸引子調控
吸引子調控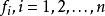 吸引子調控
吸引子調控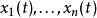 吸引子調控
吸引子調控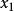 吸引子調控
吸引子調控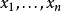 吸引子調控
吸引子調控其中,u(t)是外界的控制輸入與原有布爾網路同步。函式 為n元邏輯函式。 為節點在第t時刻的狀態值。 系統實質上就是帶輸入的布爾控制網路。在系統中被控制的節點為 。在實際研究中,被控制的節點可以是 中的任意一個。
定理1:
根據半張量積理論將系統)線性化為如下的形式:
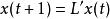 吸引子調控
吸引子調控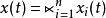 吸引子調控
吸引子調控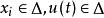 吸引子調控
吸引子調控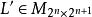 吸引子調控
吸引子調控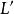 吸引子調控
吸引子調控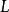 吸引子調控
吸引子調控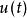 吸引子調控
吸引子調控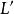 吸引子調控
吸引子調控其中 , , 。 矩陣是 矩陣在外部輸入 控制下的效果, 矩陣是受控下的狀態轉移矩陣。
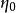 吸引子調控
吸引子調控 吸引子調控
吸引子調控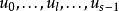 吸引子調控
吸引子調控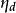 吸引子調控
吸引子調控如果布爾網路的初態為 ,則在長度為 的控制輸入序列 的調控下,系統可以達到的狀態為 ,若且唯若:
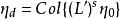 吸引子調控
吸引子調控由定理1可知在確定布爾網路的初始狀態和輸入序列後可以獲得系統的可達狀態集合。
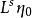 吸引子調控
吸引子調控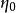 吸引子調控
吸引子調控當計算 我們可以得到布爾網路在沒有輸入控制時,以 為初始狀態運行s時刻後可以達到的狀態。有如下結論。
定理2:
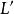 吸引子調控
吸引子調控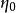 吸引子調控
吸引子調控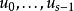 吸引子調控
吸引子調控設有布爾網路,當它沒有外界輸入時,其狀態空間可以用$L$矩陣描述,當它有外界輸入時,其狀態空間可以用 矩陣描述。當 為初始狀態,控制輸入為 ,s為輸入序列的長度,這個輸入序列為有效輸入序列的判別條件為:
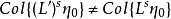 吸引子調控
吸引子調控定理2說明只有布爾網路的可達狀態集合發生改變,輸入序列才是有效的。
套用
吸引子調控的基本方法:
1、確定吸引子的調控狀態下的最大的可達狀態集合
2、判斷吸引子轉換的可達性
3、如果可達再計算控制序列的長度,最後確定起始狀態、目的狀態和控制序列
按照上述步驟布爾網路在控制序列調控下每—時刻的狀態都能被確定。
近年來吸引子調控已經取得了一些成績。比如研究人員採用比較評估的方法確定卵巢癌中潛在的藥物靶點 。另外—種有目的的吸引子調控方法在擬南芥花的器官上得到套用 。