定義
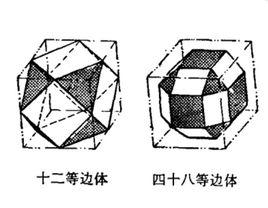
多面體的多面角都契約，當這些多面角由兩種(及)以上正多邊形構成，則多面體稱為半正多面體。例如把正四面體一條棱各三等分，沿三等分點從原體割去四個小正四面體，餘下的多面體就成為半正多面體，它的多面角都契約，這些多面角都由1個正三角形，2個正六邊形構成。這一半正多面體我們記為3·6 。
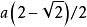半正多面體阿基米德發現了全部13個可能的所謂半正多面體。正多面體的面都是同一類型的正多邊形，而半正多面體是一個凸多面體，它的面也是正多邊形，但並非全都是同一種類型。例如，如果我們從一個立方體a的8個角上各切掉一個邊長為的四面體，結果得到的圖形就是一個半正多面體，或稱阿基米德多面體，其表面由8個等邊三角形和6個正八邊形構成 。
種類
命題半正多面體（表1）有13種：
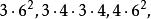半正多面體
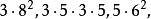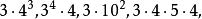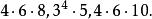半正多面體
半正多面體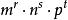
半正多面體
半正多面體我們用表示每一多面角由r個正m邊形，s個正n邊形，t個正p邊形構成的半正多面體 。
| 種類 | 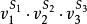 半正多面體 | 面數F | 頂點數V | 棱數E | 體積為1的棱長 |
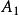 半正多面體 | 3·6 | 8 | 12 | 18 | 0．717 |
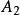 半正多面體 | 3·4·3·4 | 14 | 12 | 24 | 0．445 |
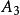 半正多面體 | 4·6 | 14 | 24 | 36 | 0．263 |
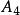 半正多面體 | 3·8 | 14 | 24 | 36 | 0．419 |
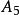 半正多面體 | 3·5·3·5 | 32 | 30 | 60 | 0．227 |
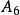 半正多面體 | 5·6 | 32 | 60 | 90 | 0．486 |
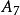 半正多面體 | 3·4 | 26 | 24 | 48 | 0．751 |
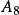 半正多面體 | 3·4 | 38 | 24 | 60 | 0．417 |
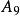 半正多面體 | 3·10 | 32 | 60 | 90 | 0．287 |
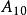 半正多面體 | 3·4·5·4 | 62 | 60 | 120 | 0．502 |
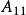 半正多面體 | 4·6·8 | 26 | 48 | 72 | 0．296 |
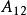 半正多面體 | 3·5 | 92 | 60 | 150 | 0．288 |
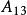 半正多面體 | 4·6·10 | 62 | 120 | 180 | 0．169 |
命題 半正多面體只有13種。
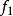半正多面體
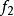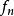半正多面體
半正多面體證明我們記每一多面角頂點圍繞s個正多邊形，其中s₁個正r₁邊形，s₂個正r₂邊形，......s個正r邊形，s=s+s+...+s，又設此半正多面體中共有個正r₁邊形，個正r₂邊形，....，個正r邊形，則
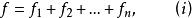半正多面體而
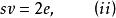半正多面體又
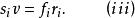半正多面體把(i)~ (iii)代人Euler示性數公式v+f=e+2，並進行整理，得到半正多面體的特徵方程 ：
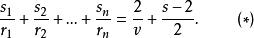半正多面體性質
半正多面體有以下性質:
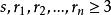半正多面體性質1，這是顯然的 。
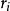半正多面體性質2中至少有一個應小於6。
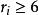半正多面體證明 反證法。如果所有，那么特徵方程將是：
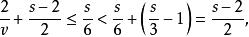半正多面體故v<0，引起矛盾。
性質3s<6。
證明直接從特徵方程計算，由性質1得
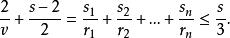半正多面體
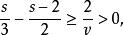半正多面體解得s<6。
綜合性質1和性質3，我們有
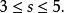半正多面體（更加細緻的討論請參考相應書籍）。
