編碼介紹
FEC編碼的冗餘部分允許接收方檢測可能出現在信息任何地方的有限個差錯，並且通常可以糾正這些差錯而不用重傳。FEC使接收方有能力糾正錯誤而不需要反向請求數據重傳，不過這是以一個固定的更高轉發的頻寬為代價的。因此FEC被套用在重傳開銷巨大或者不可能重傳的情況下，比如單向通信連結的時候以及以多路廣播的形式傳送數據給多個接收方時。FEC信息通常被添加到大量存儲設備中，以保障受損數據的恢復。FEC也被廣泛套用在調製解調中。
接收方利用FEC處理一個數字比特流或對一個數字調製載波進行解調。在後一種情況下，FEC是接收方模擬信號與數位訊號轉換的一個必要部分。Viterbi解碼器完成了一個軟判決算法從受噪聲干擾的模擬信號中解調數字數據（FEC的解碼方式分為硬判決解碼和軟判決解碼兩種。硬判決FEC解碼器輸入為0，1電平，由於其複雜度低，理論成熟，已經廣泛套用於多種場景；軟判決FEC解碼器輸入為多級量化電平。由於硬判決解碼損失了接收信號中所含的有關信道差錯統計特性的信息，軟判決解碼通常性能要優於硬判決解碼 ）。許多FEC編碼器還能生成一個誤比特率（BER）信號，這個信號能用作一個反饋，以此調整模擬信號接收設備。
噪聲干擾信道的編碼理論建立了在給定噪聲水平下信道數據傳輸率的理論最大值限界。有些高級FEC系統已經非常接近理論最大值。
可被糾正的差錯數量和丟失比特的最大值是由FEC的編碼方式決定的，因此不同的前向糾錯碼適合不同的套用場景。在一個碼組集合中，任意兩個碼字之間對應位上碼元取值不同的位的數目定義為這兩個碼字之間的漢明距離。任意兩個編碼之間漢明距離的最小值稱為這個碼組的最小漢明距離。最小漢明距離是碼的一個重要參數，它是衡量碼檢錯、糾錯能力的依據。最小漢明距離越大，碼組越具有抗干擾能力。假設d表示漢明距離，當滿足d>=e+1時，可檢測e個位的錯誤；當滿足d>=2t+1時，可糾正t個位的錯誤；當滿足d>=e+t+1時，可糾正t個錯，檢測e個錯。
工作方式
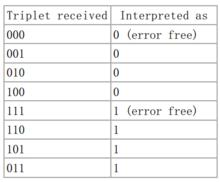前向糾錯編碼技術FEC是基於一種算法給傳輸的信息添加冗餘部分來實現的。一個冗餘位的值或許是原始信息中許多信息位的一個複雜函式。編碼之後，原始信息或許按原樣存在，或許不再按原樣存在。如果原始信息原樣包含在輸出的編碼中，這樣的編碼就是系統的，否則就是非系統的。 一個最簡單的FEC的例子就是每個數據位發三次，也就是所謂的（3,1）重複碼。經過一個存在噪聲的信道傳輸後，接收者或許會看見8個版本的輸出，如右圖所示。
這種方法允許三位中的任意一位發生錯誤，發生錯誤時通過“多數投票”來糾錯。這種FEC的糾錯能力局限於：
•每組最多一位出錯，或者
•每組最多兩位丟失（上表中沒有包含這種情況）
儘管這種方式簡單且套用廣泛，但是這種3倍冗餘的編碼是非常低效的。更好的前向糾錯碼典型地根據最後接收到的幾百個比特來決定如何對當前的一小組比特（通常2到8比特一組）進行解碼。
平均噪聲
FEC可以說是靠“平均噪聲”工作的；由於每一個數據位影響多個傳輸標誌位，即使一些標誌位因噪聲受損，我們依舊可以利用其它依賴於相同用戶數據的未受損標誌位得到原始的用戶數據。
•由於這種風險共擔的效應，當信噪比高於某個最小值時，使用FEC的數據通信系統往往表現良好
•這種孤注一擲的傾向——懸崖效應，就像很多更健壯的編碼器使用的那樣，越來越接近於理論上的香農限界
•當信道差錯往往是突發產生的時候，交叉FEC編碼可以減輕傳輸FEC編碼的孤注一擲的傾向。但是這種方法有局限性：它最好用於窄頻帶數據
大多數數據通信系統使用一種固定的信道編碼，這種信道編碼設計可以處理預期的最壞誤比特率，但是當誤比特率更糟糕時就會完全失效。一些系統可以自適應給定的信道錯誤率水平，其中有一些把FEC和ARQ方式結合起來，稱為混合糾錯方式。ARQ方式在傳送端採用某種能發現一定程度傳輸差錯的簡單編碼方法，對所傳信息進行編碼，加入少量監督碼元，接收端則根據編碼規則，對收到的編碼信號進行檢查，一量檢測出有錯誤時，即向傳送端發出詢問的信號，要求重發。傳送端收到詢問信號時，立即重發已發生差錯的那部分信息，直到接收端正確收到為止。在混合糾錯方式中，只要FEC可以處理當前錯誤率，就使用一種固定的FEC方法，當錯誤率太高時，就切換成ARQ方式。另外的自適應調製和編碼方式使用了各種各樣的FEC率，當信道中的錯誤率上升時就給每個包加上更多的糾錯位，當不需要它們的時候就拿下來。
編碼類型
主要有兩種FEC碼——分組碼和卷積碼。
•將信源的信息序列分成獨立的塊進行處理和編碼，稱為分組碼。編碼時將每k個信息位分為一組進行獨立處理，變換成長度為n（n>k）的二進制碼組。分組碼用於固定大小的比特塊（包）或預知大小的符號。分組碼的解碼時間和組的長度呈多項式關係，它將信源的信息序列分成獨立的塊進行處理和編碼。
•若以（n,k,m）來描述卷積碼，其中k為每次輸入到卷積編碼器的bit數，n為每個k元組碼字對應的卷積碼輸出n元組碼字，m為編碼存儲度，也就是卷積編碼器的k元組的級數，稱m+1= K為編碼約束度m稱為約束長度。卷積碼將k元組輸入碼元編成n元組輸出碼元。卷積碼用於任意長度的比特流或符號流。儘管有時也用其他算法，但是最常用的軟判決算法是Viterbi算法。隨著卷積碼約束長度的增加，Viterbi解碼可以達到近似最佳的解碼效率，但是這是以成倍增加的編碼複雜度為代價的。卷積碼和分組碼的根本區別在於，它不是把信息序列分組後再進行單獨編碼，而是由連續輸入的信息序列得到連續輸出的已編碼序列。進行分組編碼時，其本組中的n-k個校驗元僅與本組的 k 個信息元有關，而與其它各組信息無關；但在卷積碼中，其編碼器將k個信息碼元編為n個碼元時， 這n個碼元不僅與當前段的k個信息有關，而且與前面的（m－1）段信息有關。
有許多種分組碼，在經典的分組碼中，最著名的是Reed-Solomon碼，因為它被廣泛使用在雷射唱片、DVD和硬碟驅動器中。其他類型的經典分組碼包括格雷碼、BCH碼、多維奇偶校驗碼 和漢明碼。
漢明碼 被廣泛用於快閃記憶體的糾錯。它提供了一位糾錯和兩位檢錯。漢明碼只適用於更可靠的單層式存儲快閃記憶體。更密集的多層快閃記憶體要求更強大的多位糾錯碼，例如BCH碼和Reed-Solomon碼。NOR快閃則典型地不使用任何糾錯。
經典的分組碼通常使用硬判決算法解碼，這意味著對於每一個輸入輸出信號，硬判決取決於它對應的是1還是0 。與此形成對比的是，卷積碼使用Viterbi、MAP或BCJR等軟判決算法解碼，這些算法離散地處理模擬信號，比硬判決算法的糾錯效果更好。
幾乎所有經典分組碼都適用於有限域的代數性質。因此，經典分組碼通常被稱為代數碼。
和經常說明檢錯或糾錯能力的經典分組碼相比，許多現代分組碼（如LDPC碼）缺乏這樣的保證。另外，現代分組碼靠誤比特率進行評估。
大多數的前向糾錯都只糾正位翻轉，而不是位插入或位刪除。在這種背景下，漢明距是衡量誤比特率的合適方法（把兩個碼組中對應位上數字不同的位數稱為碼組的距離，簡稱碼距。碼距又稱漢明距離）。有一些前向糾錯碼是專門用來糾正位插入或位刪除的，比如Marker Codes 和 Watermark Codes。當使用這一類的編碼時，編輯距離是一種更為合適的用來衡量誤比特率的方式（編輯距離（Edit Distance），又稱Levenshtein距離，是指兩個字串之間，由一個轉成另一個所需的最少編輯操作次數。許可的編輯操作包括將一個字元替換成另一個字元，插入一個字元，刪除一個字元）。
級聯碼
對於有進行多次編碼的系統，對各級編碼，看成一個整體編碼，稱為級聯碼。經典的（代數的）分組碼和卷積碼通常會在級聯碼中合併使用。其中，有限長度的卷積碼負責大部分的工作，組長度更大的分組碼抹去任何卷積解碼器造成的錯誤。使用這一類糾錯碼的單通道解碼可以獲得很低的錯誤率，但是在遠距離傳輸（比如外太空）的條件下更推薦疊代解碼。
自從旅行者2號探測器在1986年飛向天王星的時候首次使用級聯碼以來，級聯碼已經成為衛星和外太空通信的標準編碼。
Turbo碼
從香農信道編碼定理 可知，要達到或接近信道容量極限，應該採用無限長的隨機碼，而解碼應該採用最大似然解碼。但是，採用隨機編碼，使碼長趨於無窮大並且採用最大似然解碼將會使系統的複雜度和延時變得太大，無法在實際中使用。因此，必須研究新的編碼方案。目前能夠逼近香農容量極限的是被稱為Turbo-like的一類碼，包括Turbo碼、LDPC碼、RA碼等。這類碼的特點在於部分地引入了隨機編碼的思想，並且它們的碼長都較長，解碼均採用了接近最大後驗機率解碼的疊代解碼算法。
Turbo碼是一種疊代軟判決方案，它也是一種級聯碼。它把幾種簡單的卷積碼和交叉器組合起來產生一種分組碼。它的性能可以部分達到香農極限。在實際運用方面，Turbo碼先於LDPC，它們現在提供相似的性能。Turbo碼最早的商業用途是高通公司的數字行動電話技術CDMA2000 1x。
Turbo碼的性能遠遠超過了其他的編碼方式，得到了廣泛的關注和發展，並對當今的編碼理論和研究方法產生了深遠的影響，信道編碼學也隨之進入了一個新的階段。目前Turbo碼的研究尚缺少理論基礎支持，但是在各種惡劣條件下（即低SNR情況下），提供接近香農極限的通信能力已經通過模擬證明。
LDPC
低密度奇偶校驗碼（LDPC）是由許多奇偶校驗碼組成的線性分組碼，它是一種級聯碼。人們最近重新發現了它的高性能。它使用一種疊代的軟判決解碼手段，能提供接近於理論最大值的信道容量，時間複雜度與組的長度呈線性關係。它的實際實現嚴重依賴於組成它的奇偶校驗碼的並行解碼。
LDPC最先是由Robert G. Gallager在他1960年的博士論文中提出。但是由於編碼器和解碼器的計算成就和里德·所羅門碼的問世，它被人們長期忽視，直到最近才被重視。
LDPC最近被用於許多高速通信標準中，比如DVB-S2 (數位電視廣播)、WiMAX (IEEE 802.16e微波通信標準)、 高速無線區域網路(IEEE 802.11n)。
局部解碼
有時我們只需要對信息中的幾位進行解碼，或者只是查看一個給定的信號是否是編碼字而不用查看整個信號。在數據流的背景下就是這樣，編碼字太大了，無法快速解碼，而信息中只有幾位是有用的。這樣的編碼已經成為計算複雜性理論中的重要工具，例如機率可驗證明。
對於可以局部解碼的編碼來說，即使編碼字的一部分已經被損壞了，仍然可以通過查看編碼字的一小部分就恢復幾位信息。對於可以局部檢測的編碼來說，可以通過查看信號的一小部分判斷該信號是否接近一個編碼字。
交叉編碼
交叉編碼技術被廣泛套用在數字通信和存儲系統，用於改進前向糾錯碼的性能。許多信道不是無記憶的：錯誤通常是突發的而不是獨立的。如果碼字中的錯誤數量超過了糾錯碼的能力，那就無法恢複數據了。
交叉編碼技術通過讓信號分布在多個碼字內來改善這個問題，因此就導致了錯誤的平均分布。所以交叉被廣泛用於突發糾錯。對於渦輪碼來說，交叉器是必備的部件，它的適當設計對於提高性能非常重要。當代表解碼器的因子圖中沒有短的環路時，疊代解碼算法性能最優；交叉器可以用來避免出現短的環路。
在多載波器通信系統中，載波器間的交叉用於提供頻率隔離以及減輕頻率選擇性衰減、窄頻帶干擾。
實例
圖一是沒有使用交叉編碼的傳輸。
圖一這裡，每一組4個字母代表一個4位的糾錯碼字。碼字cccc被改掉了一位，可以被糾正。但是dddd被改了3位，無法對其解碼或正確解碼。
圖二是使用交叉編碼的傳輸。
圖二在每一組碼字aaaa,、eeee、 ffff、 gggg中，只有一位被更改，所以一位糾錯碼可以正確地進行解碼。
圖三是沒有使用交叉編碼的傳輸。
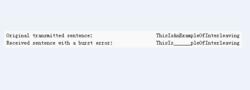圖三最終單詞“AnExample”因為多個字母數據損壞，無法被識別，難以糾正。
圖四是使用交叉編碼的傳輸。
圖四雖然有突發錯誤，但是沒有一個詞是完全被破壞的，丟失的字母可以靠猜測恢復。
交叉技術的不足
使用交叉技術增加了總體時延。這是因為必須收到整個交叉塊後才能對數據包解碼。另外，交叉器隱藏了錯誤的結構。與交叉器和簡單的解碼器配合使用相比，更先進的解碼算法可以利用錯誤的結構實現更可靠的通信。
刪除碼
在使用先進刪除碼的情況下，數據和前向錯誤糾正信息被編碼到每個數據塊內。要恢複數據，系統必須先獲取編碼系統所要求的最小數量以上的數據塊，然後將這些數據塊解碼以恢複數據。一個CleverSafe系統的要求是，每存儲16個數據塊，起碼需要有10個塊才能進行解碼並滿足讀取請求。
使用先進刪除碼的系統對數據塊有最小數據量要求，然後再將數據塊予以解碼。這樣做會大幅增加系統的計算負荷。這裡需要指出的是它會增加小型寫入的開銷，因為還沒有被覆蓋的數據需要被解碼，然後結合完新數據後再重新編碼。
因此，我們已經討論過的所有使用高水平刪除碼的系統都採用向外擴展架構。給每4到18個磁碟驅動器配置一個Xeon處理器可以讓這些使用複雜ECC方式的系統有足夠的能力處理數據的編碼和解碼。傳統中端陣列中每800多個磁碟驅動器才有4個Xeon處理器，很難應付這樣的計算開銷。
FEC列表
| 距離 | 編碼 |
| 2（檢測單位錯） | 奇偶校驗碼 |
| 3（糾正單位錯） | 三重模組冗餘碼 |
| 3（糾正單位錯） | （7,4）漢明碼 |
| 4（單錯校正雙錯檢測） | 擴展漢明碼 |
| 5（雙錯糾正） | |
| 6（雙錯糾正/三錯檢測） | |
| 7（三錯糾正） | 二進制戈萊碼 |
