概述
在分形樹索引中,內部(非葉)節點可以具有在某個預定義範圍內可變數量的子節點。當數據從結點插入或刪除時,其子節點的數量會更改。為了維持預定義的範圍,內部節點可能被連線或拆分。B樹的每個內部節點將包含比其分支因子小一個的多個鍵。鍵作為分割其子樹的分割值。子樹中的鍵按搜尋樹順序存儲,即子樹中的所有鍵位於兩個包圍值之間。在這方面,它們就像B樹。 分形索引樹好B樹都利用了這樣的事實:當從存儲器中獲取結點時,獲取其大小由B指示的存儲塊。因此,節點被調整為大約為B的大小。由於對存儲器的訪問可以支配數據結構的運行時間,外部存儲器算法的時間複雜度由讀/寫一個數據結構的數量誘導。 (參見例如[7]用於以下分析)
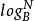 分形樹索引
分形樹索引在B樹中,這意味著幾點鐘的鍵的數量的目標是足以填充節點,具有用於節點分裂和合併的一些變化性。為了理論分析的目的,如果O(B)鍵適合一個節點,樹具有深度o( ),這是搜尋和插入的I/O複雜性。
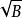 分形樹索引
分形樹索引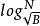 分形樹索引
分形樹索引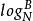 分形樹索引
分形樹索引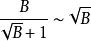 分形樹索引
分形樹索引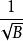 分形樹索引
分形樹索引分形樹節點使用較小的分支因子,例如 ,樹的深度是O( )=O( ),從而漸進地匹配B樹,每個節點中的剩餘空間用於緩衝插入,刪除和更新,我們將其稱為訊息。當緩衝區充滿時,他們被批量分配給子樹。對於如何刷新緩衝區有幾個選擇,都導致類似的I/O複雜度。節點緩衝區的每個訊息由其鍵決定將被刷新到特定的子樹,假設,為了具體性,訊息被刷新到同一個子樹,並且在子樹中,我們選取有最多訊息的那一個。然後至少有 訊息可以刷新到子樹。每次刷新需要O(1)刷新,因此每個訊息刷新的代價為O( )。
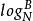 分形樹索引
分形樹索引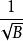 分形樹索引
分形樹索引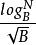 分形樹索引
分形樹索引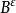 分形樹索引
分形樹索引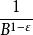 分形樹索引
分形樹索引考慮到插入的成本,每個訊息刷新 次,每次的代價是 。因此,插入的成本是O( )。最後,注意分支因子可以變化,但對於任何分支因子 ,刷新的成本是 。從而在搜尋代價上順利提供了權衡,這取決於搜尋樹的深度,因此分支因子對插入時間有關,插入時間取決於樹的深度,但是對緩衝區刷新的大小更加敏感。
索引比較
此部分將分形樹索引與其他外部存儲器索引數據結構進行比較。關於這個主題的理論文獻非常大,因此本討論僅限於與資料庫和檔案系統中使用的流行數據結構進行比較。
B樹
B樹的搜尋時間與分形樹索引的搜尋時間漸近相同。然而,分形樹索引具有比B樹更深的樹,並且如果每個節點需要I/O,則說如果快取是稀少的,則分形樹索引將引起更多的IO。然而,對於許多工作負載,B樹和分形樹索引的大多數或所有內部節點已經快取在RAM中。在這種情況下,搜尋的成本由獲取葉的成本支配,這在兩種情況下是相同的。因此,對於許多工作負載,分形樹索引可以在搜尋時間方面匹配B樹。
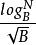 分形樹索引
分形樹索引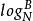 分形樹索引
分形樹索引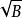 分形樹索引
分形樹索引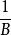 分形樹索引
分形樹索引它們不同的是插入,刪除和更新。分形樹索引中的插入需要O( )然而B樹需要O( )。因此,分形樹索引比B樹快了O( )倍。由於B可能相當大,這在最壞情況下的插入時間產生潛在的兩個數量級的改進,這在實踐中觀察到。在最好的情況下,B樹和分形樹索引都可以更快地執行插入。例如,如果按順序插入鍵,則兩個數據結構都實現O( )IOs每次插入。因此,由於B樹的最佳和最差情況差別很大,而分形樹索引總是接近其最佳情況,因此分形樹索引在B樹上實現的實際加速取決於工作負載的細節。
合併樹
日誌結構合併樹(LSMs)是指一類數據結構,其由指數級增長容量的兩個或更多個索引結構組成。當某個級別的樹達到其容量時,它被合併到下一個更大的級別。 LSM的IO複雜性取決於參數,例如級別之間的生長因子和在每個級別選擇的數據結構,因此為了分析LSM的複雜性,我們需要選擇一個特定的版本。為了比較,我們選擇與分形樹索引匹配的插入性能的LSM的版本。
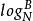 分形樹索引
分形樹索引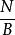 分形樹索引
分形樹索引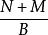 分形樹索引
分形樹索引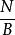 分形樹索引
分形樹索引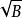 分形樹索引
分形樹索引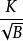 分形樹索引
分形樹索引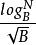 分形樹索引
分形樹索引假設LSM是通過O()B樹實現的,每個樹都具有大於其前身的容量,合併時間取決於三個事實:N項目B樹中的鍵的排序順序可以在O()IOs構建。N和M項的兩個排序列表合併到一個排序列表中需要O() IOs;N個項目的排序列表的B樹可以在O()構建。當樹溢出時,它被合併成一個大小為原來O()大的樹,因此有k項等級的需要O()IOs來合併。每個級別可以合併一個項,總時間為O(),這與分形樹索引相匹配。
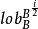 分形樹索引
分形樹索引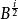 分形樹索引
分形樹索引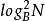 分形樹索引
分形樹索引查詢時間只是每個級別的B樹查詢時間。第i級的查詢時間是O()=(i),由於第i級容量為,所以總時間是O().這比B樹和分形樹索引大了一個對數級因子。事實上,雖然B樹和分形樹索引都在插入和查詢之間的最佳權衡曲線上,但是LSM不是。它們與B樹無法比較,並且由分形樹索引控制。
關於LSMs的一些注意事項:有辦法使查詢更快。例如,如果只需要成員身份查詢,並且沒有後繼/前導/範圍查詢,那么Bloom過濾器可以用於加速查詢。此外,級別之間的生長因子可以被設定為某個其他值,給出插入/查詢權衡的範圍。然而,對於插入率的每個選擇,相應的分形樹索引具有更快的查詢。
Bε樹
分形樹索引是Bε樹的細化。像Bε樹一樣,它由帶鍵值和緩衝區的節點組成,並實現最優的插入/查詢權衡。分形樹索引在包括性能最佳化和擴展功能方面不同。改進的功能的示例包括ACID語義。 ACID語義的B樹實現通常涉及鎖定活動事務中涉及的行。這樣的方案在B樹中工作良好,因為插入和查詢涉及將相同的葉子節點提取到存儲器中。因此,鎖定插入的行不會導致IO損失。但是在分形樹索引中,插入是訊息,並且行可以同時駐留在多個節點中。因此分形樹索引需要一個單獨的鎖定結構,它是IO高效的或駐留在記憶體中,以便實現ACID語義所涉及的鎖定。
分形樹索引也有幾個性能最佳化。首先,緩衝區本身被編入索引以加快搜尋速度。第二,葉子比在B樹中大得多,這允許更大的壓縮。事實上,葉子被選擇為足夠大,使得它們的訪問時間由頻寬時間支配,並且因此分期尋找和旋轉延遲。大葉子是大範圍查詢的優點,但點查詢較慢,這需要訪問葉子的小部分。在分形樹索引中實現的解決方案是具有可以作為整體被提取為快速範圍查詢的大葉子,但也可以被分成更小的片段可以單獨提取的基底節點。由於頻寬時間減少,訪問基本節點比訪問葉節點更快。因此,與Bε樹相比,分形樹索引中的葉子的子結構允許快速的範圍和點查詢。
索引操作
插入,刪除和更新作為訊息插入緩衝區,使它們朝向葉子。 可以利用訊息基礎設施可以被運用到實現各種其他操作,下面討論其中一些操作。
更新插入
更新插入是一個語句,用於插入一個行(如果不存在),如果存在,則更新它。在B樹中第一次搜尋行的時候完成更新插入,然後根據搜尋結果完成插入或者更新。這需要將該行提取到記憶體中,如果它沒有被快取。分形樹索引可以通過插入特殊的更新訊息來實現更新插入。理論上,這樣的訊息可以在更新期間實現任意代碼段。在實踐中,支持四種更新操作:
1. x =常數
2. x = x +常數(廣義增量)
3. x = x - 常數(廣義遞減)
4. x = if(x = 0,0,x-1)(底線為0的遞減)
這些對應於LinkBench中使用的更新操作[8],這是Facebook提出的一個基準。通過避免初始搜尋,更新插入訊息可以以數量級提高更新插入的速度。
模式更改
到目前為止,所有訊息類型都修改了單行。但是,複製到所有傳出緩衝區的廣播訊息可以修改資料庫中的所有行。例如,廣播訊息可用於更改資料庫中所有行的格式。雖然改變所有行所需的總工作量相對於遍歷表的強制性方法沒有改變,但是延遲被改進,因為一旦訊息被注入到根緩衝器中,所有後續查詢能夠將修改的模式套用到他們遇到的任何行。模式改變是立即的,並且工作被推遲到緩衝器溢出和葉子節點需要更新的時間。
實現
分形樹索引已經實現並由Tokutek商業化。 它可用作TokuDB作為MySQL和MariaDB的存儲引擎,以及作為TokuMX,與MongoDB的更完整的集成。 分形樹索引也已經在原型檔案系統TokuFS中使用。[4]
