簡介
八次函式是 高次函式的一類,由於其複雜程度,在實際的運用中出現機會很少。即使在函式的泰勒級數展開中也很少展開到八次。但是其性質的討論足以讓我們感受到數學的美妙,鍛鍊我們的思維能力。它沒有一般性的零點解法,或者說,一元八次方程不存在一般性的求解公式。事實上當方程最高次數大於等於5時,不存在這樣的公式。這最早由阿貝爾和伽羅瓦完成證明。
性質
對稱性
八次函式的對稱性並不具有一般性,對於它的係數的不同取值會出現不同的結果。它的對稱性一般藉助現有的作圖工具或軟體直接觀察。例如八次函式:
 八次函式
八次函式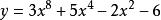 八次函式
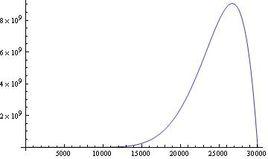
八次函式由圖可見,直線x=0是它的對稱軸。但是由於係數選取的特殊性,它在給定作圖的區間內的圖像十分平緩,這並不影響我們尋找它的一條對稱軸方程。
按照八次項係數到常數項的順序,將其分別取作
{0.5,-0.6,-1.2,9,-6.7,-30,100,-1000}
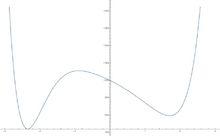 八次函式
八次函式獲得函式圖像如右圖。可以觀察到圖像的變化,這在八次甚至更高次數的函式中更能體現。此時它不具備對稱性。
局部極值
由於八次函式是多個冪函式乘上一個給定的係數之後的和,這些冪函式的最高次數是8。我們引入和式來改寫八次函式即:
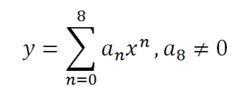 八次函式
八次函式我們對y求導,得到y',根據冪函式的求導法則,我們能得到的是:
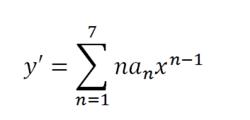 八次函式
八次函式根據冪函式的根的存在性判定,我們知道y'至多有七個零點,但這七個零點的解析解不能獲得,但我們可以找到近似解。事實上,前面給出的兩個圖像也是運用類似的方法做出局部極值的位置。找到這樣的零點後,帶入到原方程中我們得到的就是在八次函式y上的局部極值點。這樣的結論是顯然的。所以有:
n次函式至多存在n-1個局部的極值。