定義
低速流是指可以忽略流體密度變化影響的流動。一般指馬赫數小於0.3的流動。
密度與馬赫數的關係
真實流體都具有程度不同的可壓縮性,但液體的壓縮性很小,流動中的壓強變化不足以引起明顯的密度變化(水下爆炸、水擊等情況除外),因而液體流動一般都屬不可壓縮流動。氣體流動中的密度變化可按歐拉方程分析:
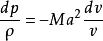 低速流
低速流式中Ma是馬赫數,ρ、v分別是密度和速度。若Ma很小,則密度變化可以忽略,屬不可壓縮流動範疇 。若Ma不很小,如大於0.3,則密度變化不可忽略,屬可壓縮流動。在不可壓縮流動中,流動參數通常僅為速度和壓強;但在可壓縮流動中,還須增加密度,並伴隨溫度。變數增加了,控制方程的數目和求解的複雜性也增加了。可壓縮流動按馬赫數大小可分為亞聲速流動(Ma=0.3~0.8左右)、跨聲速流動(Ma=0.8~1.2左右)、超聲速流動(Ma=1.2~5.0左右)和高超聲速流動(Ma>5.0)。高速飛行器和太空飛行器的飛行馬赫數大多遠超過0.3 ,其繞流問題都必須按可壓縮流動的理論處理。
近三十年來,隨著高速飛行、噴氣發動機、火箭、空間飛行、彈道學、燃燒學、燃氣渦輪、衝壓噴氣發動機、傳熱學等方面的發展,可壓縮流動理論的研究取得了巨大進展,已成為一個重要的科學領域。
不可壓縮流
不可壓縮流是密度不發生變化的流體運動。而定常是指流體和時間無關。確切地說, 是流體在一個大時間段後某一時刻的狀態或者趨於穩定的狀態。為了實用的目的,假設流體在流動時為不可壓縮流體。在低速下,這大體上是對的;但是,甚至對於液體,速度的急劇變化也會產生壓縮或者膨脹。通常,液體在重力作用下流動,因而在一個開放容器中它占據著較低的部分。這一性質是液體獨具的特性。相反,氣體可壓縮地流動,不管氣體和空間的初始容積有多大,它都占據整個限制它的任何封閉空間。這一性質是氣體所特有的。像液體的情況一樣,對氣體的緩慢流動採用不可壓縮的假設可以獲得良好的近似結果。特別地, 它的研究對人們認識和控制湍流至關重要。描述這種流體的控制方程主要有不可壓縮Navier–Stokes方程,還有不可壓縮Stokes方程以及Stokes特徵值問題。
分析不可壓縮流常常以對無粘性或“完全”流體的解附加上流體粘性效應的方法加以分析。像均勻流、源、匯和渦這樣一些簡單的流動,可以用確定流動速度的數學表達式表示出來。這些解可以疊加起來,以表達像在空氣中運動的機翼或在水中運動的船體這樣一些實際的複雜無粘性流。結果得到流場中所有點上的速度的大小和方向的數學表達式。然後通過伯努利方程,可以把流動中某一點上的壓力(P)與速度(v)聯繫起來。這樣,由壓力引起而作用在邊界上的力就可以計算出來。然後,餘下的問題就是確定粘性如何影響流場和壓力分布,以及流體摩擦引起的平行於邊界的附加力。在不可壓縮流這一領域中,粘性起著重要的作用,因為它決定了靠近流動邊界的流體(邊界層)的行為,以及流體不沿著邊界流動的區域(分離區)中的流體行為。雷諾數,即流體中慣性力和粘性力的無量綱比值,給出流動特性的一個量度,它對於把實驗數據和理論聯繫起來是十分有用的。

