似群元素

似群元素是余代數中與群代數中的群元素性質類似的元素。設 (C,△,ε) 是 R 余代數，c∈C，若 ∆(c)=c⊗c ，則稱 c 是似群元素。

定義

似群元素是余代數中與群代數中的群元素性質類似的元素。

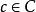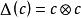似群元素

似群元素

設 (C,△,ε) 是 R 余代數，，若，則稱 c 是似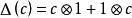群元素。

似群元素

若 C 是雙代數且，則稱 c 是本原元素。

余代數

余代數(coalgebra)是代數的對偶概念。

設 C 是 R 模， Δ 是一個 R 線性映射 C→CC ，被稱為余乘法或對角映射； ε 是一個 R 線性映射 C→R ，稱為余單位元或增廣。

R上的余代數是指滿足以下二交換圖的三元組(C，Δ，ε)：

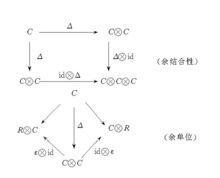余代數

雙代數

雙代數是指一種代數系統。

它既有代數結構，又有餘代數結構，且兩種結構具相容性。設(B，μ，η)是R代數，且(B，Δ，ε)是R上的余代數，其中μ是B的乘法映射，η是刻畫B的單位元的映射。若Δ和ε都是R代數同態(等價於μ，η都是R余代數同態)，則(B，μ，η，Δ，ε)稱為R上的雙代數。