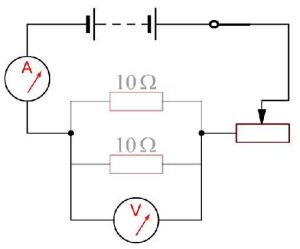
並聯電阻的計算公式:
電流計算
I總=I1+I2+......+In
即總電流等於通過各個電阻的電流之和
電壓計算
U總=U1=U2=Un
並聯電路各支路兩端的電壓相等,且等於總電壓
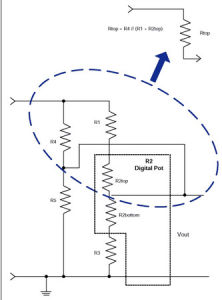 並聯電阻
並聯電阻電阻值計算
1/R總=1/R1+1/R2+1/R3+......+1/Rn
即總電阻的倒數等於各分電阻的倒數之和
對於n個相等的電阻串聯和並聯,公式就簡化為R串=n*R和R並=R/n
用圖解法求並聯電阻
方法一
若要求R1與R2的並聯電阻值,可先作直角坐標系xOy,並作Y=X的直線l,在OX軸上取A點,使OA長度等於R1的阻值,在OY軸上取B點,使OB長度等於R2的阻值,連結AB與直線l相交於M點,則M點的坐標(X或Y)值即為R1與R2的並聯阻值。
證明:作MD⊥OX
∵△aob∽△ADM
∴AO/BO=AD/DM
因OD=DM,並設其長度為R的數值
R1/R2=(R1-R)/R
解得:R=R1R2/(R1+R2)
此即R1、R2的並聯電阻的阻值。
套用若需求三個電阻的並聯電阻值,可先求R1、R2的並聯電阻,得到D點,再在OY軸上取C點,使OC長度等於R3的值,連CD與l直線交於N點,則N點的坐標值為R1、R2、R3的並聯總阻的阻值。例如,令R1=4Ω,R2=12Ω,R3=6Ω,求解結果為圖2所示,R1、R2的並聯總阻為3Ω,R1、R2、R3的並聯總阻為2Ω。
方法二
在平面上任取一點O,用相互交角為120°的三矢量作為坐標軸OX、OY、OZ(
 並聯電阻
並聯電阻證明面積S△AOB=S△AOC+S△BOC
即(1/2)AO×BO×Sin120°
=(1/2)AO×OC×Sin60°+(1/2)BO×OC×Sin60°AO×BO=AO×OC+BO×OCR1R2=R1R+R2R
∴R=R1R2/(R1+R2)
套用可方便地連續求解多個電阻的並聯值。例如,若要求R1、R2、R3的並聯總阻的阻值,只需先求出R1、R2並聯後的阻值R12(即得到C點),再在OA的負向取一點D,快OD長等於R3的值,連結CD交OY軸於E點,則OE長即為R1、R2、R3的並聯總阻的阻值,如圖3。如R1=4Ω,R2=12Ω,R3=6Ω,按此法可求出R12=3Ω;R1、R2、R3三電阻並聯電阻值為2Ω,如圖4。
以上求解方法對於求電容器串聯、彈簧串聯,凸透鏡成象等與電阻並聯有相似計算公式的問題,同樣適用
性質
串聯電路的特點
歐姆定律:I=U/R
變形求電壓:U=IR
變形求電阻:R=U/I
電壓的關係:U=U1+U2
電流的關係:I=I1=I2
電阻的關係:R=R1+R2
並聯電路的特點
電壓的關係:U=U1=U2
電流的關係:I=I1+I2
電阻的關係:1/R=1/R1+1/R2
電功的計算:W=UIt
電功率的定義式:P=W/t
常用公式:P=UI
焦耳定律:Q放=I2Rt
對於純電阻電路而言:Q放=I2Rt=U2t/R=UIt=Pt=UQ=W
照明電路的總功率的計算:P=P1+P1+……