簡介
下降法亦稱極小化方法，是一類重要的疊代法。這類方法將方程組求解問題轉化為求泛函極小問題。
類型
最速下降法
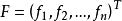下降法設給出方程組 F(x)=0，其中，令
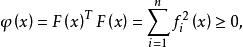下降法則 F(x)=0 的充分必要條件是φ(x)=0. 若φ(x) 的極小點 x* 使φ(x*)=0，則 x* 也是方程組 F(x)=0 的解。只要構造疊代序列 {x } 使
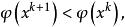下降法且滿足
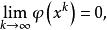下降法就可求得方程組的足夠好的近似解。
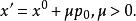下降法
下降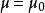法
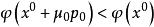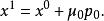下降法
下降法具體做法是選初始近似 x ，沿一個使φ(x) 下降的方向 p，令 然後選步長因子，使，得一般情況是從 x 出發，沿φ(x) 下降方向 p 求出
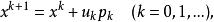下降法
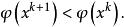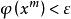下降法
下降法且 直到為止，x 就作為方程組解 x* 的近似，上述算法中也可選 uk 使
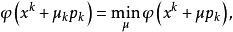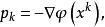下降法
下降法這是一個求一維的極小問題。以上算法即為下降法。如果 p 選擇不同，就可得到不同的下降法，特別地，若選 p為 φ 的負梯度，即則得梯度算法
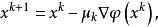下降法其中
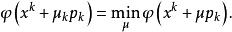下降法此算法也成最速下降法，此法的優點是計算量少，程式簡單，但收斂慢。在下降法中可去下降方向 p 為牛頓方向，即
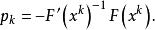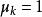下降法
下降法特別地，當 時，就得到牛頓法，此外還可取沿坐標方向下降的方法，實際上就是一步的 SOR 牛頓法。
共軛梯度法
另一類較重要的下降法為共軛梯度法。共軛梯度法是最簡單的下降法，早在 1847 年就由法國數學家、力學家柯西 (Cauchy,A.-L.)提出，以後坦普爾 (Temple,G.)、柯里 (Curry,H.) 等人也進行過研究並證明了方法的收斂性。20世紀50至60年代，又有不少學者對下降法做了很多研究，提出不少具體算法並建立了收斂性理論，使這類算法在解非線性方程組和最最佳化計算中得到廣泛套用。
