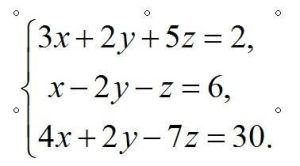概念
含有三個相同的未知數,每個方程中含未知數的項的次數都是一次,叫做三元一次方程組。方程組中,少於3個方程,則無法求所有未知數的解,故一般的三元一次方程是三個方程組成的方程組。
解法
解三元一次方程組的基本思路是:通過“代入”或“加減”進行消元,將“三元”化為“二元”,使解三元一次方程組轉化為解二元一次方程組,進而再轉化為解一元一次方程。
他們主要的解法就是加減消元法和代入消元法,通常採用加減消元法,若方程難解就用代入消元法,因題而異。其思路都是利用消元法逐步消元。
步驟:①利用代入法或加減法,消去一個未知數,得出一個二元一次方程組;
②解這個二元一次方程組,求得兩個未知數的值;
③將這兩個未知數的值代入原方程中較簡單的一個方程,求出第三個未知數的值,把這三個數寫在一起的就是所求的三元一次方程組的解。
學習目的與要求
1.了解三元一次方程組的概念;能熟練掌握簡單的三元一次方程組的解法;能選擇簡便的解法解特殊的三元一次方程組。
2.能通過用代入消元法,加減消元法解簡單的三元一次方程組,及選擇合理,簡捷的方法解方程組,培養運算能力。
3.通過對方程組中未知數係數特點的觀察和分析,明確三元一次方程組解法的主要思路是"消元",從而促成未知向已知的轉化,培養和發展邏輯思維能力。
4.能將三元一次方程組通過消元轉化為二元一次方程組,再消元轉化為一元一次方程及將一些代數問題轉化為方程組問題,初步運用轉化思想去解決問題,發展思維能力。
套用
三元一次方程簡單套用:
1.{x+2y+z=7①
2x-y+3z=7②
3x+y+2z=18③},解x,y,z值。
解:①+②×2得:5x+7z=21④
②+③得:x+z=5⑤
聯立④、⑤得:
{5x+7z=21
x+z=5
利用二元一次方程解法解得:
{x=7
{z=-2
把x=7,z=-2代入①,可解得y=1
所以原方程組的解為:
{x=7,y=1,z=-2}
三元一次方程複雜套用:
2.{a1x+b1y+c1z=d1
a2x+b2y+c2z=d2
a3x+b3y+c3z=d3}組:
x,y,z未知數,a1,a2,a3,b1,b2,b3,c1,c2,c3,d1,d2,d3為常數,解x,y,z值。
{a1x+b1y+c1z=d1①
a2x+b2y+c2z=d2 ②
a3x+b3y+c3z=d3③}
解:{b1y=d1-a1x-c1z④
b2y=d2-a2x-c2z⑤
b3y=d3-a3x-c3z⑥}
④÷⑤
b1/b2*(d2-a2x-c2z)=d1-a1x-c1z⑦
⑤÷⑥
b2/b3*(d3-a3x-c3z)=d2-a2x-c2z⑧
由⑦得:
b1/b2*d2-b1/b2*a2x-b1/b2*c2z=d1-a1x-c1z
a1x-b1/b2*a2x+c1z-b1/b2*c2z=d1-b1/b2*d2
(a1-b1/b2*a2)x+(c1-b1/b2*c2)z=d1-b1/b2*d2
(c1-b1/b2*c2)z=d1-b1/b2*d2-(a1-b1/b2*a2)x⑨
由⑧得:
b2/b3*d3-b2/b3*a3x-b2/b3*c3z=d2-a2x-c2z
a2x+c2z-b2/b3*a3x-b2/b3*c3z=d2-b2/b3*d3
(a2-b2/b3*a3)x+(c2-b2/b3*c3)Z=d2-b2/b3*d3
(c2-b2/b3*c3)Z=d2-b2/b3*d3-(a2-b2/b3*a3)x⑩
⑨÷⑩
[(c1-b1/b2*c2)÷(c2-b2/b3*c3)]*[d2-b2/b3*d3-(a2-b2/b3*a3)x]=d1-b1/b2*d2-(a1-b1/b2*a2)x⑾
在⑾中a1,a2,a3,b1,b2,b3,c1,c2,c3,d1,d2,d3都是常數,只有X是未知數,所以X值已解。把常數代入式中求出X值,再將X值代入⑨或⑩,求出Z值,再將X Z值代入原式①②③中的一個,求出y值。
三元一次方程中x,y,z三個未知數值已解。