歷史
兩個n位數相乘的標準程式需要許多與n 成比例的基本運算，或者採用big-O表示法的O（n ）。 Andrey Kolmogorov推測經典算法是漸近最優的，這意味著該任務的任何算法都需要Ω（n ）個基本運算。
1960年，Kolmogorov在莫斯科國立大學組織了一次關於控制論數學問題的研討會，在那裡他陳述了Ω（n ）猜想和計算複雜性的其他問題。在一周之內，當時一名23歲的學生Karatsuba發現了一種算法（後來被稱為“分而治之”），它在O（n ）基本步驟中乘以兩個n位數，從而反駁猜想。科爾莫戈羅夫對這一發現非常不滿;他在研討會的下次會議上進行了溝通，然後終止了會議。 Kolmogorov在世界各地的會議上做了一些關於Karatsuba結果的講座（例如，參見“1962年數學家國際會議論文集”，第351-356頁，以及“國際數學家大會上發表的6篇講座”）在斯德哥爾摩，1962年“）並於1962年在蘇聯科學院院刊上發表了該方法。這篇文章由Kolmogorov撰寫，包含兩個關於乘法的結果，Karatsuba算法和Yuri Ofman的單獨結果;作為作者，它列出了“A. Karatsuba和Yu.Onman”。 Karatsuba在收到出版商的重印時才發現了這篇論文。
算法
基本步驟
Karatsuba算法的基本步驟是允許人們使用三個較小數字的乘法來計算兩個大數x和y的乘積的公式，每個乘數大約是x或y的一半，加上一些加法和數字移位。 事實上，這個基本步驟是高斯複數乘法算法的推廣，其中虛數單元i被基數的冪代替 。
設x和y在某個基數B中表示為n位字元串。對於任何小於n的正整數，可以將兩個給定的數字寫為：
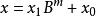Karatsuba算法 
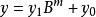Karatsuba算法 
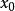Karatsuba算法 
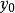Karatsuba算法 
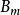Karatsuba算法 其中 和 小於 。 那么就是:
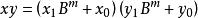Karatsuba算法 
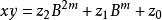Karatsuba算法 這裡
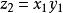Karatsuba算法 
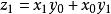Karatsuba算法 
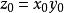Karatsuba算法 
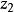Karatsuba算法 
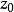Karatsuba算法 這些公式需要四次乘法，並且Charles Babbage知道。Karatsuba觀察到xy只能在三次乘法中計算，但需要額外增加幾次。 如前所述， 和 可以計算出來。
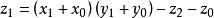Karatsuba算法 從那以後
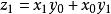Karatsuba算法 
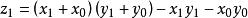Karatsuba算法 
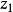Karatsuba算法 
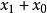Karatsuba算法 
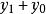Karatsuba算法 然而，當計算 時發生的問題是上述 和 的計算可能導致溢出（將產生0≤x≤B的範圍內的結果） m，需要乘法器有一個額外的位。
例子
要計算12345和6789的乘積，選擇B = 10和m = 3.然後我們使用得到的基（Bm = 1000）分解輸入運算元，如下所示：
12345 = 12 · 1000 + 345
6789 = 6 · 1000 + 789
只有三個乘法運算較小的整數，用於計算三個部分結果：
z = 12 × 6 = 72
z = 345 × 789 = 272205
z = (12 + 345) × (6 + 789) − z − z = 357 × 795 − 72 − 272205 = 283815 − 72 − 272205 = 11538
我們通過添加這三個部分結果得到結果，相應地移位（然後通過在輸入運算元中分解基數1000中的這三個輸入來考慮進位）：
result = z · B + z · B + z,
result = 72 ·1000*1000 + 11538 · 1000 + 272205 = 83810205.
注意，中間第三乘法對輸入域進行操作，該輸入域小於兩次第一次乘法的兩倍，其輸出域小於四倍，並且必須從前兩次乘法計算得到的base-1000進位 計算這兩個減法時的帳戶。
z = 283815 − 72 − 272205 = 11538.
